My Blogs
P6809 [BalticOI 2010 Day2] Mines
17k 的含金量。
设 $c_{i,j}$ 表示答案,$a_{i,j}$ 表示输入数据。
首先可以确定 $c_{3,3}=a_{2,2}-a_{2,1}-a_{1,2}+a_{1,1}$,
用二维差分可以知道 $c_{i,j},c_{i-3,j},c_{i,j-3},c_{i-3,j-3}$ 的关系,这样就能推出来 $c_{a,b}$,其中 $a,b\equiv 0\pmod 3$。
这样利用了左上角的东西,然后右上右下左下也是一样的,所以可以确定出来 $i\equiv 0/n-2\pmod 3$,$j\equiv 0/m-2\pmod 3$ 的所有格子 $c_{i,j}$。
然后如果 $n-2,m-2$ 都不是 $3$ 的倍数,这样就知道了整个矩阵:

黑色格子是上面知道的。知道了所有黑色格子之后深灰色的格子也是可以求出来的(依靠同一条边边上两个相邻 $a$ 的差分可以知道相邻两个格子的和,如 C2 和 C1 的和就是 $a_{1,2}-a_{1,1}$,然后 C1 因为已经知道了,所以也能知道 C2)。最后在填浅灰色的格子,没填的直接给他填上就行了。
对于 $n-2$ 不是 $3$ 的倍数但是 $m-2$ 是的情况,首先画出来能直接确定的格子:

还是用二维差分,观察能确定那些格子:

容易发现这样信息已经“满了”,即不可能再确定任何一个格子。但是这样可以用一维差分知道相邻两个数的和,也能知道跨过一条黑线的相邻两个数的和(如 $c_{3,1}+c_{3,2}+c_{3,3}=a_{2,2}-a_{1,2}$,然后 $c_{3,3}$ 已经确定,这样就能知道 $c_{3,1}+c_{3,2}$。然后 $c_{6,1}+c_{6,2}+c_{6,3}-c_{3,1}-c_{3,2}-c_{3,3}=a_{5,2}-a_{4,2}$,$c_{3}$ 的和也知道了,所以就能知道 $c_{6,1}$ 和 $c_{6,2}$ 的和……依此类推)。
然后显然只保留相邻两个数的和的限制就能满足原限制。所以如果和是 $0$ 或者 $2$ 就直接填,这样图上会剩若干条链,链上满足相邻的都是 $01,10$ 即可。
对于 $n-2,m-2\equiv 0\pmod 3$:
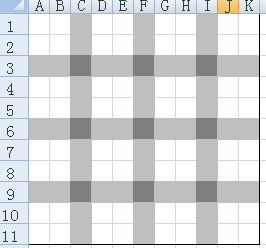
十分不牛,只能确定一些单点的确切值。但是相邻两个浅灰色格子的和以及跨过一个黑色格子的两个相邻浅灰色格子的和都是知道的,所以可以用和第二种情况类似的方法确定出灰色格子的和的。
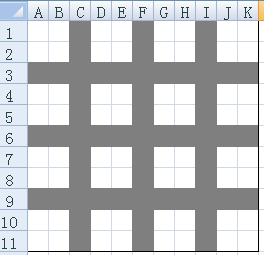
然后这样只能知道相邻四个的一个田字格的数的和了,忽然发现这个是经典问题矩阵游戏的弱化版,直接粘个 spfa 上来就过了。