IOI 赛制!最有素质的一集!
Day 1
T1
什么 B 题。
首先对 $p$ 从大到小排序,一定取一段前缀做。暴力 DP $f_{i,j}$ 表示前 $i$ 个做对了 $j$ 个。可以证明有值的项不会特别多(???),大概是 $\mathcal O(\sqrt{n\log{\epsilon^{-1}}})$ 级别的,所以暴力就过了。
模拟赛场上写了一个非常不牛的分块 FFT,但是 luogu 上似乎被卡精度了。首先每个位置可以看成一个 $(p_i+(1-p_i)x)$ 的多项式。序列分块,处理出 $F_i$ 表示前 $i$ 个块多项式的乘积,块内用上面的暴力 DP。拼起来的时候前缀和优化一下即可做到 $\mathcal O(n\sqrt{n\log n})$。
还讲了一个很牛的分治。设 solve(l,r,F) 表示要处理区间 $[l,r]$,然后 $[1,l-1]$ 的所有多项式乘起来是 $F$。
对于 $[x^i]F$,如果 $i-(r-l+1)>k$,那这个 $f_i$ 在区间里一定有贡献,直接加到区间里面就行了。如果 $i+(r-l+1)<k$,那这个 $f_i$ 在区间里一定没有贡献,所以需要考虑的项只有 $[k-(r-l+1),k+(r-l+1)]$ 里面的,所以 solve 需要保留的多项式长度就是 $\mathcal O(r-l+1)$ 级别的。这样 FFT 一下就可以做到 $\mathcal O(n\log^2 n)$ 求出每一项的答案了。
T2
参考炫酷原神。
首先如何判一个子序列是否:把串扔进子序列自动机里,找到尽可能往前匹配的话,每个字符 $i$ 匹配到了哪个位置 $p_i$。如果存在相邻两个 $p_i,p_{i+1}$,满足 $(p_i,p_{i+1})$ 里面出现了一个和 $p_i$ 颜色相同的数,那就一定合法。容易发现这个条件是充要的。
看上去很像什么矩乘优化。从后向前 DP,$f_{i,j,0/1}$ 表示考虑了 $[i,n]$ 这个后缀,选的第一个数颜色是 $j$(注意 $j$ 所在的位置一定是 $i$ 后面第一次出现 $a_k=j$ 的位置 $k$),是否已经合法的方案数。
转移非常麻烦的分类讨论一下:首先是 $f_{i-1,\not=a_i,0/1}$ 都可以转移到 $f_{i,\not=a_i,0/1}$,表示不选这个 $a_i$。
而如果选了 $a_i$,那就是 $f_{i-1,j,k}$ 转移到 $f_{i,a_i,k\vee(t_{a_i}<t_j)}$,$t_{x}$ 表示 $x$ 这个颜色第一次在 $[i+1,n]$ 中的出现位置。
还有 $f_{i,a_i,t_{a_i}==n+1}$ 需要加一。$=n+1$ 表示后面没有出现过。
容易发现上面的转移满足了子序列自动机的条件,即一定是能靠前匹配就靠前匹配的。
转移可以写成大小为 $13$ 的矩阵,并且修改一个位置最多会修改 $m+1$ 个地方的矩阵(修改位置 $x$ 前面每一个颜色的最后一次出现位置的矩阵都有可能发生变化),但是两个矩阵相乘实际上不用乘这么多项,因为 $f_{\ast,1}$ 不可能转移到 $f_{\ast,0}$,并且常数项也不会变,加上一些神秘剪枝(比如判断矩阵实际上有没有改变,线段树修改 $m$ 个位置最后只 update 一次),实际是能跑过的。复杂度 $\mathcal O(nD(m)+qmD(m)\log n)$。其中 $D(m)$ 表示矩阵乘法需要的时间,剪枝之后可以达到 $3m^3$ 左右。
T3
遗憾离场。看上去像个分析性质题,实际上比较暴力。
首先暴力从后向前模拟,维护 $f_i$ 表示当前想让这个人同意的话,需要分给他 $f_i$ 个金币。显然从小到大选,复杂度是 $\mathcal O(n^2\log n)$。
核心性质是每个人分得的钱数一定不会超过 $\max(a)$(记为 $w$)。在 $i\rightarrow i-1$ 的时候,只需要令 $S_{i-1}=[i-1,n]\setminus S_i$,$S_i$ 是第 $i$ 个人的答案。
所以用线段树维护集合 $A_{i,j}$ 表示如果当前想让他同意,需要花费 $i$ 个金币,贪婪值等于 $j$ 的点的位置集合。
处理到 $i$ 的时候,从小到大枚举金币数量,什么时候需要的总和大于 $m$ 了或者人数合法了就停下。然后很讨厌的限制是金币相同的话编号从大到小选,所以确定了给出的最大金币数 $k$ 后,$<k$ 的所有人都要选,然后所有 $=k$ 的人选的是一段后缀。所以在所有 $A_{k,\ast}$ 上同时进行一个线段树二分,即可找出需要的区间。
这样操作就是,对于不选的人,金币数全部归零,然后所有人的金币数都加上各自贪婪值。这里会发生若干合并和分裂,需要线段树合并和分裂实现。这样是 $\mathcal O(na^2\log n)$ 左右。
注意到一个人清零之后,金币数就一定是他自己贪婪值的倍数,所以对于还没被清零过的数暴力处理(一个人最多被暴力处理 $256/a$ 次),这样复杂度可以优化到 $\mathcal O(n(a\log a+w(a)\log n))$,实际远远跑不满。
Day 2
T1
太魔怔了。
首先如果一个 $2\times 2$ 的矩形都是 $1$ 那就消不掉。找出所有这样的,剩下消不掉的形如若干条蛇。直接维护这个即可。
T2
判定区间 $[i,j]$ 是否合法:把 $[i,j]$ 内的设成最大值,其余设成最小值,设 $s_k$ 表示 $[1,k]$ 的前缀和,要求 $s_{i-1}$ 是前缀最小值,$s_{j}$ 是后缀最大值,$[i,j]$ 之间不存在前缀和小于 $s_{i-1}$ 的,也不存在前缀和大于 $s_j$ 的。这几个条件都可以简单处理,形如 $r\geq f_l,l\leq f_r$。
但是还有一个限制是,$i$ 左边的和 $[i,j]$ 不交的区间以及 $j$ 右边的和 $[i,j]$ 不交的区间的和需要小于等于 $[i,j]$ 的和。这个乍一看似乎没有单调性,虽然 $nex_r$(即 $[r+1,n]$ 的最大子段和)是单调的,但是 $s_r-s_{l-1}$ 并不单调。但是因为钦定了 $s_r-s_{l-1}$ 就是 $[l,r]$ 的最大子段和,所以可以取一个前缀 $\max$,这样两个函数都有单调性了,二分即可。所以最终限制还是形如 $r\geq f_l,l\leq g_r$。可以 BIT 统计,复杂度 $\mathcal O(n\log n)$。
T3
Day 3
小赢一手。
T1
简单题,一个边双里的数肯定需要全部相同。然后可以断开一条链,每个连通块内部颜色相同。看成每个大小为 $s$ 的连通块有 $\frac 1 2 s(s-1)$ 的贡献,要求总贡献尽量小。
然后 DP,设 $f_i$ 表示断了 $i$ 子树内的一个根链,同时断了 $(i,fa_i)$ 这条边,贡献最小值。然后统计答案就是枚举 $i,j$,贡献是 $f_i+f_j+\frac 1 2(n-siz_i-siz_j)(n-siz_i-siz_j-1)$,拆开之后是斜率优化的形式,上个李超树就行了。
T2
暴力是不断合并两个子树。问题变成两个有序序列如何归并到一起。可以用决策单调性分治加二分的方式得到很多分。
T3
爱拼才会赢。拼指拼暴力。
首先可以预处理一下,封装一个 $A(v,l)$ 表示有一个 $B$ 中的区间,最小值是 $v$,长度是 $l$,和 $A$ 中的任意一段拼起来的答案。单次查询复杂度 $\mathcal O(\log n)$。
然后对于 $B$,找出其所有笛卡尔树区间。被查询区间包含的是好算的。困难的是有交的。
序列上建线段树,从右向左扫,扫到一个点就把挂在这个点上的笛卡尔树区间加到线段树里。查询也在若干线段树节点里查询。
可以发现有决策单调性???然后维护一个决策栈就行了。
Day 4
T1
每个格子建一个点,然后建循环一样的图:
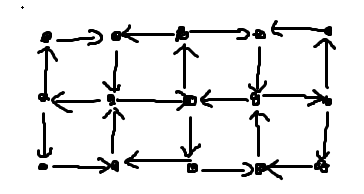
容易发现图上的一个圈是满足题目要求的。但是这样每个点可能会流好几次(就是一个格子里有四条边),只需要拆入点和出点限制一下流量就行了。题目要求一个格子有边的限制,所以是上下界最大费用循环流。
T2
T3
Day 7
T1
那我咋办?
首先一个位置要么是左边会向右扔球,要么右边向左扔球,要么两种都不操作。根据不操作的位置划分成若干区间,每个区间是一段前缀需要往左,一段后缀需要往右。
现在唯一的问题在于,中线上的球不知道哪些往左哪些往右。如果这个确定了,则可以用一个简单的堆进行贪心:首先左右独立,以左侧为例,维护大根堆表示当前球的所有代价,加入这个位置的所有球,然后放下代价最大的球。
考虑另一种等价的操作:维护 $L_i$ 表示需要 $i\rightarrow i-1$ 位置的球数,从小到大,每个球向左找到最远的能放到的位置,这个也是对的。
一个观察是,上面操作最终 $L$ 的状态之和操作了哪些位置有关,和操作顺序无关。然后就可以 DP 了。
T2
取 $x=10^5$,则 $query(x,y)$ 是关于 $y$ 分段的凸函数。而且因为 $x$ 足够大,所以函数的转折点不交,所以求出函数的转折点就可以求出所有函数:假设有一个转折点在 $Y$,则有一条直线 $y=\lfloor\frac Y {10^5}\rfloor x+(Y\bmod 10^5)$。
如何求转折点?维护这个凸函数区间两端的直线的方程,找到这两条的交点,查询这个交点。如果询问出来的值恰好等于交点的函数值,则就找到了这个凸函数的一个拐点,找到一条直线并返回,否则通过两次询问找到中间这个直线的方程,往两侧递归。
T3
这题真菜吧/ng/ng/ng。
建出 SAM,求出 $f_i$ 表示 $i$ 这个节点开头的串的数量。
从前向后一位一位确定字符,可以把问题转化为查询以当前串 $C$ 为前缀的两个串拼起来的串的数量。第一种是 $C$ 是 $S$ 这部分的串的前缀,这部分是简单的,查询 $S$ 的 SAM 中的 $f$,乘上 $T$ 中本质不同子串数量。
麻烦的是 $C$ 不是 $S$ 的前缀。那就需要查询 $\sum_{1<j\leq k}C[j,k]$ 在 $T$ 的 SAM 上走完之后能接的 $f$ 的数量。注意到这是 $T$ 的后缀树上的一段前缀,预处理一下即可。细节比较多。
Day 8
T1
相当于若 $c_i=c_j$,则连边 $(i,j,\max(\lvert x_i-x_j\rvert,\lvert y_i-y_j\rvert))$,否则连边 $(i,j,\min(\lvert x_i-x_j\rvert,\lvert y_i-y_j\rvert))$。
第二类是好处理的,$x,y$ 两维是独立的,分别排序后,先把坐标相同的点缩起来,然后找到每个同色连续段,按如下方式连边:
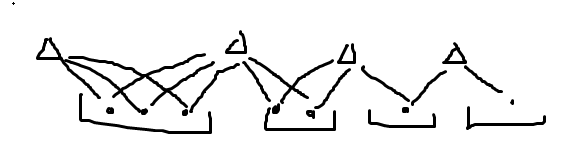
对于第一类,唐氏想法是也是优化建图,转曼哈顿距离后分治连边:
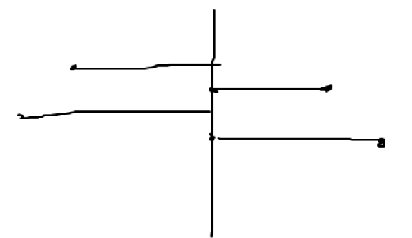
但是注意到如果走了一类边,则只会是从起点直接走一步。这样只需要跑二类边的图然后最后整体 check 一遍就行了。
T2
先考虑判定。如果要生成一个 $v$,则是需要操作一下 $[v-1]$,这样可以调成每个数出现次数都不少于需要的出现次数。现在若某个数出现过多,可以先操作变成 $0$。然后显然可以同时操作几个 $0$ 然后再操作一个 $1$ 来使 $0$ 的数量任意减少,但是需要大于等于 $1$。
但是如果要求 $0$ 的出现次数是 $0$ 呢?如果存在任意一次 $[v-1]$ 的操作则已经合法了,因为可以把多出来的这些 $0$ 和他一起操作。否则考虑第一个不为 $0$ 的数 $k$,若 $0$ 的个数 $\geq 2^{k-1}-1$ 则合法。这是操作一下 $k$,这样有 $2^{k-1}$ 个 $0$,可以归纳证明这是生成一个 $k$ 最小需要的 $0$ 的个数。那先把 $0$ 的数量减少到 $2^{k-1}-1$ 即可。
考虑直接对上述过程计数。从后向前依次确定每个数最终在集合中的出现次数,$f_{i,j,k}$ 表示确定了 $[i+1,300]$ 的出现次数,当前需要 $[i]$ 操作 $j$ 次,同时后面多了 $k$ 个点变成 $0$。转移是简单的。状态数是 $n^2\log n$ 调和级数,转移可以前缀和优化到 $\mathcal O(1)$。这样可以计数除了最后有 $0$ 但是需要没有 $0$ 的所有情况。
对于最后一种情况,可以暴力随便算算。
T3
首先显然一个点的答案一定是一个矩形。
定义一个矩形是好的当且仅当他的四条边上都全是 $1$,并且内部每一行,每一列都至少有一个 $0$。可以证明矩形的数量是 $\mathcal O(nm)$ 的,枚举上边界,左右两条边是笛卡尔树区间数,下边界也是唯一的。
找出所有矩形后,一个点的答案就是包含它的最小矩形。随便弄弄就行了。
Day 9
说的道理。阿巴阿巴。
T1
死妈了。首先如果问了 $p[1,n]$,则可以确定,只有 $p_i=weigh(P)-\sum p$ 的 $i$ 才有可能是假币。按照 $a$ 从小往大扫,设 $b_i$ 表示前面 $p_j=i$ 的 $j$ 的个数,每次选择 $b$ 最小的加进去就是对的。
T2
$f_{i,j}$ 表示 $i$ 上填 $j$ 的方案数。问题在于合并,叶子儿子先不管他,找一个分界点 $v$,可以证明一定存在一个 $v$ 使得 $v+#[>v]$ 比较小。然后在这上面状压就行了。
T3
首先最小生成树可以写成如下线性规划形式:
\[\min_{y\in \mathbb{R}^{E}}\sum_{i\in E}c_iy_i,\;\;\;\;\;\;\;\text{subject to}\;\;\;\;\; \begin{cases} \begin{aligned} &\sum_{i\in E}y_i=n-1\\ &\sum_{i\in E(S)}y_i\leq \lvert S\rvert -1\;\;\;(\forall S\subseteq [n],S\not=\emptyset)\\ &y_i\geq 0\;\;\;\;\;(\forall i\in E) \end{aligned} \end{cases}\]将上述问题的可行域记为 $P_{st}\subset \mathbb R^{E}$。原题即为:
\[\max_{x\in \mathbb{R}_{+}^{E}}\min_{y\in P_{st}}K\sum_{i\in E}(c_i+x_i)y_i-\sum_{i\in E}d_ix_i\]由 minmax 定理(??),min 和 max 的顺序可以互换(??)
\[\min_{y\in P_{st}}\max_{x\in \mathbb{R}_{+}^{E}}\sum_{i\in E}(Ky_i-d_i)x_i+K\sum_{i\in E}c_iy_i\]因为有 $(Ky_i-d_i)x_i$ 这一项,所以一定有 $Ky_i-d_i<0,x_i=0$,否则内层就是正无穷。所以问题变为:
\[\min_{y\in P_{st}}K\sum_{i\in E}c_iy_i,\;\;\;\;\; \text{subject to}\;\;\;\;\;Ky_i\leq d_i\]变形一下,令 $y_i\leftarrow Ky_i$,即为
\[\min_{y\in \mathbb{R}^{E}}K\sum_{i\in E}c_iy_i,\;\;\;\;\;\text{subject to}\;\;\; \begin{cases} \begin{aligned} &\sum_{i\in E}y_i=K(n-1)\\ &\sum_{i\in E(S)}y_i\leq K(\lvert S\rvert -1)\;\;\;(\forall S\subseteq [n],S\not=\emptyset)\\ &0\leq y_i\leq d_i\;\;\;\;\;(\forall i\in E) \end{aligned} \end{cases}\]然后问题就变成了类似 CF1951I。结论是从小到大考虑 $c_i$,保证合法的情况下加入尽量多的加入这条边就是对的。
考虑如何处理第二个限制,这其实是一个最大权闭合子图。假设考虑到 $i$,限制是:
\[\sum_{j\in E(S)}y_j\leq K(\lvert S\rvert -1)\;\;\;\;\;(\forall \{a_i,b_i\}\subseteq S\subseteq [n])\\ y_i\leq K(\lvert S\rvert -1)-\sum_{j\in E(S),j\not=i}y_j\;\;\;\;\;(\forall \{a_i,b_i\}\subseteq S\subseteq [n])\\\]要求右侧的最小值,看成求 $\sum y_j-K\lvert S\rvert$ 的最大值。对于左侧点 $i$,向右侧点 $a_i,b_i$ 连流量为 $+\infin$ 的边,对于已经确定了 $y$ 的点源点向左侧点 $i$ 连流量为 $y_i$ 的边,对于右侧点 $j$ 向汇点连流量为 $K$ 的边。同时要求了左侧点 $i$ 必须选,所以源点向左侧点 $i$ 连流量为 $+\infin$ 的边。这样 $\sum y_i-K-\text{maxflow(G)}$ 即为 $\sum y_j-K\lvert S\rvert$ 的最大值,所以令 $y_i=\min(\text{maxflow(G)}-K-\sum y_j,d_i)$ 即可。
Day 10
T1
唐氏。
显然要容斥,枚举一个点集求包含他的正方形的面积和。发现如果点集围成的矩形的非边界上如果有至少一个点,则这个矩形的总容斥系数一定是 $0$。所以枚举矩形上边界后,从上到下扫,可以找出 $\mathcal O(n^2)$ 个矩形。现在问题就变成了 $\mathcal O(1)$ 算包含一个给定矩形的正方形面积和。
首先枚举正方形边长 $d\in[\max(x_2-x_1,y_2-y_1),\min(N,M)]$,贡献是 $d^2(\min(N-d,x_1)-max(0,x_2-d))(\min(M-d,y_1)-\max(0,y_2-d))$。拆成四段分段函数,每一段上需要自然数幂和。
T2
去你妈的。
T3
去你妈的。
Day 11
可惜。
T1
我是傻逼。
首先差分:令 $i\in[1,n+1],b_i=a_i-a_{i-1}$。然后要把所有 $b$ 调到 $0$。先把 $a,b$ 弄到互质,然后求一个 $ax_0+by_0=1$ 的特解。则第 $i$ 个位置的操作次数就是,$x_i=d_ix_0+kb,y_i=d_iy_0-ka$。要求 $\sum x_i=0,\sum y_i=0$,然后 $\sum\lvert x_i\rvert+\lvert y_i\rvert$ 最小。
$\sum x_i=0$ 和 $\sum y_i=0$ 显然只需要满足一个就都满足了。如果把每个位置的这个都取最优解的话,可能会发生 $\sum x_i\not=0$。但是此时一定有,$\lvert x_i\rvert \leq b$,所以只需要调整 $\mathcal O(n)$ 步就合法了。拿个堆或者排序维护一下就行了。
T2
烂。
首先 $d\leq \min(n,m)$ 的话,考虑求出一个图形,这个图形是一个极大团。这个转切比雪夫距离之后就是一个矩形。容易发现若 $d$ 是偶数则形状是左图,$d$ 是奇数则形状是右图。
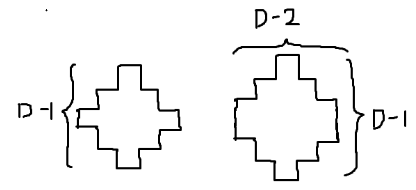
然后用这个东西做密铺就行了。其实写出来就是一个 $d$ 的循环移位。
对于 $\min(n,m)<d\leq \max(n,m)$,假设 $n>m$,密铺图形在 $m$ 是奇数是是左图,$m$ 是偶数时是右图:
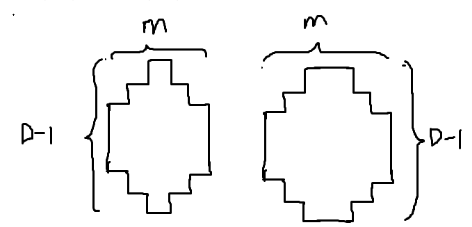
也是用这个东西做密铺。对于 $d>\max(n,m)$ 也是一样的。
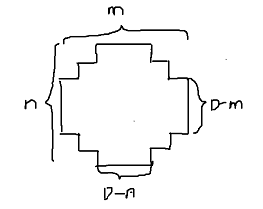
这个可能有一点小细节,比如铺不上去,可能需要把右下角再额外扩一条斜线。
T3
不可做题。首先题目可以转化为,枚举 $i\in [1,n]$,从 $1$ 到 $m$ 扫,如果 $S_i$ 是 B,并且 $b_j>a_i$,则交换 $b_j,a_i$。如果 $S_i$ 是 S 并且 $b_j<a_i$,则交换 $b_j,a_i$。
把 $S$ 相同的缩起来,每个段需要维护一个堆,B 是大根堆,S 是小根堆。每次就是往堆里面扔进去 $a_i$,然后 $a_i$ 变为堆顶,然后堆弹出堆顶。
Day 21
T1
比较简单。暴力是记录轮廓线的状态:每个点是否操作和当前是 $0$ 还是 $1$,这样是 $\mathcal O(4^m nm)$。但是注意到操作了之后,这个点对答案就没有影响了(因为可以通过把操作 $1$ 和操作 $2$ 交换来让这个点变化 $1$),所以只需要记录点的三种状态:操作了,没操作并且当前是 $1$,没操作并且当前是 $0$。覆盖掉一个点的时候,如果他最后还是 $1$,就看成在他上面操作了两次。复杂度 $\mathcal O(3^mnm)$。
T2
也比较简单。
首先称一个区间 $[l,r]$ 是好的当且仅当不存在一个子区间 $[l’,r’]$ 使得 $\text{mex}(l,r)=\text{mex}(l’,r’)$。可以证明好区间的个数是 $\mathcal O(n)$ 的。
如何找到好区间?用 vector $ve_i$ 维护所有 $\text{mex}=i$ 的区间,首先加入 $=0,1$ 的区间,然后从小到大扫描 $i$,扫到 $i$ 的时候,先对区间排序后只保留极短的区间。然后对于每个区间 $[l,r]$,找到 $l$ 前面第一个 $=i$ 的位置和 $r$ 后面第一个 $=i$ 的位置,求出新的区间的真实 mex 之后,扔到对应的 vector 里。求真实 mex 可以用一个主席树做到 $\mathacl O(\log n)$。
然后对于查询,维护 $f_{i,j}$ 表示加入了所有 $\text{mex}\geq i$ 的区间,右端点在 $j$ 时,想要包含一个区间,左端点最大是多少,这可以用一个主席树维护。查询就是先二分 $i$,然后一个线段树上二分找到合法区间数。复杂度 $\mathcal O(n\log n+m\log^2 n)$。
T3
Day 22
轻松爆零。
T1
首先如果确定了开头,算出每个序列相对开头的逆序对个数 $f_i$,按照这个排序,再求出两个相邻序列之间的逆序对个数 $g_i$。如果满足 $f_{i}=g_i+f_{i-1}$,则合法。
如何找开头?可以发现相对的逆序对数比较类似直径,所以可以套用直径的求法:先随便找一个序列,求出相对他逆序对最多的序列作为开头即可。
T2
直接停时定理,解方程需要一个主元法。
T3
不会。
Day 23
T1
首先看成是一个环,需要构造一个回路。如果没有相邻的 $1$ 就直接做完了。
然后考虑全 $1$,打表什么的发现 $n$ 是奇数不合法,否则可以 $1,2,1,2,3,4,3,4\dots$ 这样的填。
判掉全 $1$,然后把让第一个位置是 $0$,让最后一个位置是 $1$。如果 $11$ 的个数 $\bmod 4=0$,那也可以套用上面 $1,2,1,2$ 的构造再拼起来就行了。
而如果 $11$ 的个数是奇数显然无解,现在只剩下了 $\bmod 4=2$ 的情况。如果全 $1$ 段只有一个,那根据全 $1$ 时长度是 $4n+2$ 不合法猜测他就是不合法的,否则可以再两个段里面插两个门来拼起来。
T2
dfn 上分治。好像也能树剖之后,轻子树按照哈夫曼树合并。
T3
比较深刻。
首先对于二维的情况 $a=1$,显然要么是若干竖条,要么是若干横条,要么是横平竖直的网格:
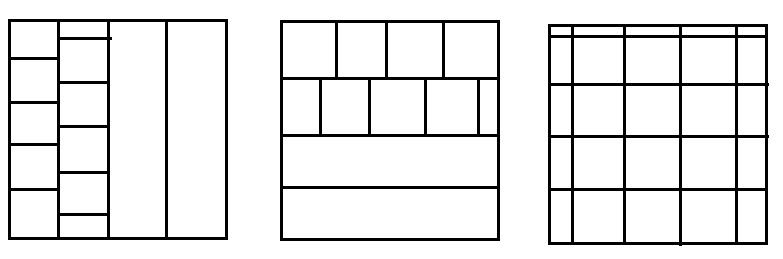
这可以简单容斥算出:$f(a,b,A,B)=ab^{A/a}+ba^{B/b}-ab$。
然后考虑三维。首先一种平凡的情况是,存在至少一个方向能把大正方体切成若干层。这个是一个简单容斥:比如钦定能切成 $A/a$ 层,每一层显然是独立的,方案数就是 $f(b,c,B,C)^{A/a}$。钦定能切 $A/a$ 和 $B/b$ 的话,就变成了若干个条,每个条的方案数是 $c$,方案数就是 $c^{A/a\times B/b}$。钦定三个方向都能切开的话就是 $abc$。
然后不平凡的情况是,三种方向都切不开。想象这个东西感觉就很困难了。考虑把他弄到二维上。
对于长方体最下面一层,设 $v_{i,j}$ 表示最下面一层的第 $i$ 行,第 $j$ 列,是被小矩形的哪一层占据的。这是 $0\sim c-1$ 之间的一个数。不能在 $z$ 轴上切开的限制就变成了,$v$ 不能全相同。
然后还有在底面矩形上,横着,纵着都不能切开的限制。手玩一下发现,一定是形如下面的情况:
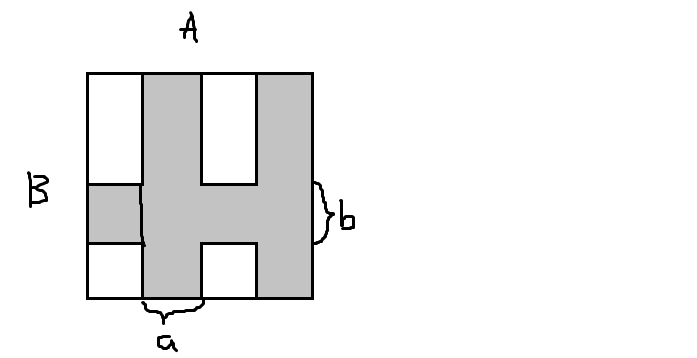
灰色的部分 $v$ 相同,然后其余的地方任意。需要在灰色的部分中放入 $a\times b$ 的小矩形来把灰色部分铺满。
只考虑灰色部分,显然仍然是分成了 $C/c$ 层,每层内填法独立。如果我们想让横着切不开,我们可以让他出现两层这样的:
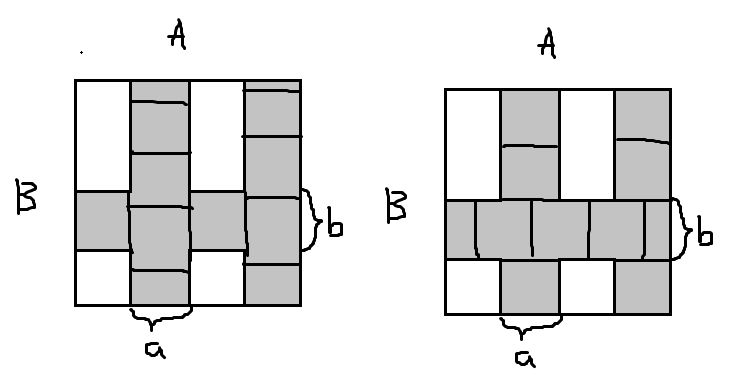
左边保证了不能横着切一刀切开,右边保证了不能竖着切一刀切开。
所以先预处理 $g_{i,j}$ 表示,灰色区域恰好有 $i$ 行 $j$ 列的方案数。这里的一行,一列指的是大的行列,一行就有 $b$ 个小行,一列就有 $a$ 个小列。这是一个二项式反演,两维分开做就是 $\mathcal O(n^3)$ 的。
然后再枚举 $g_{i,j}$,生成 $C/c$ 层使得至少有一层横着滑动了,至少有一层竖着滑动了,这也是一个简单容斥。
Day 24
T1
发现大概是要求一个 $\bmod{x^m-1}$ 意义下,$1+x^{2^i}$ 的逆。发现如果 $m$ 是奇数,那可以直接做。
然后发现 $m$ 可以不断除二。做完了。
T2
T3
每种颜色求个直径,然后随便做。