3.17
[ARC193D] Magnets
感觉很菜，比 C 菜多了。打的时候胡出来了，但是摆烂不想写。
一些简单的观察是一次操作是把一个段长度减 $2$，或者是两个相邻的段长度都 $-1$。还有一种是最左侧或者最右侧的段 $-1$，但是这种操作一定只会做一次。暴力枚举是否做左右减一的操作一共跑 $4$ 次贪心即可求出是否合法。
对于操作数，首先把区间缩成和 $b$ 的长度一样。然后除去开头结尾的操作，操作过程中中点是固定的，最后再调一下位置即可。
CF2077F AND x OR
变态。
考虑怎么判定合法。首先全相等合法，否则一定会操作一次。操作一次就能得到一个必要条件：$\exists i,j,d_i\subseteq d_j$。然后这个条件也是充分的，可以最后构造证明。
然后求出小于等于 $i$ 的最大值和次大值 $f_i,g_i$，然后做一个高维前缀和之后统计答案即可。
CF2077G RGB Walking
这太难了。
设三种边权和分别为 $f_1,f_2,f_3$，考虑求出三种颜色的所有边权分别的 $\gcd$，设为 $a,b,c$。则如果一条路径经过了所有点，则可以任意 $f_1+2a,f_2+2b,f_3+2c$。
所以首先找一棵树，遍历一遍，这样每个边都经过了 $0$ 次或者 $2$ 次，因此此时 $f_1\bmod{2a},f_2\bmod{2b},f_3\bmod{2c}$ 都是 $0$。
而从 $1$ 走到终点之后，$f_1\bmod{2a}$ 要么是 $0$ 要么是 $a$，$f_2,f_3$ 同理，一共 $8$ 种状态，所以可以求出来是否合法。
Alice, Bob, And Two Arrays
直接做。
Strong Connectivity Strikes Back
首先考虑 DAG，重边可以删到只剩一条，然后剩下的一条边能删当且仅当把他删了之后他的起点还能达到终点。
对于一个 SCC 内部，一条边删掉之后如果 SCC 不会变，那这个边一定不能删。
CF2068I Pinball
挺牛的。
考虑把图划分为若干个环，然后环之间连边权为 $1$ 的边跑最短路就是对的。阿巴阿巴。
3.19
CF2066E Tropical Season
好像不大难。
单组判定：从小到大排序，维护一个当前干净的水量 $s$。如果 $>s$ 的桶只剩不多于一个那就直接合法了。否则找到 $>s$ 的，相邻两个 $i,i+1$ 的最小差 $d$，若 $d\leq s$，则可以 $s=a_{i+1}$。然后不断进行 $s=query(1,s)$，query 返回值域在 $[1,s]$ 中的所有数的和。
拿值域线段树维护所有数，容易发现操作次数是 $\mathcal O(\log V)$ 级别的。所以复杂度是两个 $\log$。可以值域倍增分块做到单 $\log$。
CF1712F Triameter
先两边 dfs 求出 $f_i$ 表示到 $i$ 最近的叶子的距离。然后假设 $f=i$ 的集合是 $S_i$，那 $S_i$ 和 $S_j$ 之间的贡献就是 $\displaystyle \min(i+j+x,\max_{l\in S_i,r\in S_j}\text{dis}(l,r))$。
所以考虑维护当前答案 $ans$，枚举 $i$，不断尝试让 $ans$ 增大 $1$。对于 dis，可以求出点集内直径和点集后缀的直径，这样就可以用 $\mathcal O(1)$ 求了。需要一个 $\mathcal O(1)$ LCA。
CF1637H Minimize Inversions Number
非常困难。
首先对于 $k=1$，只需要找到单次贡献最大的。设 $d_i$ 表示只操作 $i$ 能让逆序对减少多少，显然 $d_i=\sum_{j<i}[a_j>a_i]-[a_j<a_i]$。这个可以简单求出来。
然后对于多组，如果选了一些 $d$，实际的意义是把选出来的子序列倒序过来拼在了最前面。所以假设选择的下标是 $p_1,p_2\dots p_k$，实际上逆序对数应该额外减去 $\sum_{i>j}[a_{p_i}<a_{p_j}]-[a_{p_i}>a_{p_j}]=\binom k 2-2\times \text{inv}(p)$。
然后核心结论是如果选择了 $i$，一定不存在 $j>i$ 且 $a_j<a_i$ 且没有选择 $j$。证明就是狂暴分类讨论。
调整法，找到 $j-i$ 最小的 $(i,j)$。尝试不选择 $i$ 并选择 $j$，对于每个 $k$，检查 $(i,k)$ 和 $(j,k)$ 的变化。
对于 $k<i$ 并且选了，$(i,k)$ 和 $(j,k)$ 相对顺序都没变，所以变化量是 $0$。
对于 $k<i$ 并且没选，$a_j<a_k<a_i$ 时，变化量是 $-2$，否则变化量是 $0$。
对于 $k>i$ 并且选了，$a_j<a_k<a_i$ 时，变化量是 $-2$，否则变化量是 $0$。
对于 $k>i$ 并且没选，$(i,k)$ 和 $(j,k)$ 相对顺序都没变，变化量是 $0$。
对于 $i<k<j$ 并且选了，一定有 $a_k<a_j$（否则 $(i,j)$ 不是最近的），变化量是 $-1$。
对于 $i<k<j$ 并且没选，一定有 $a_k>a_i$（否则 $(i,j)$ 不是最近的），变化量是 $-1$。
所以，其他所有数和 $i$ 或者是 $j$ 的逆序对数和的变化量非正。再加上 $(i,j)$ 本身的 $-1$，一定会更优。这样调整步数也一定有限。得证。
所以答案中的 $\text{inv}(p)$ 可以变为 $\sum_{i}\sum_{j>p_i}[a_{p_i}>a_j]$。是一个只和 $p_i$ 有关的值，所以算进 $f$ 里面就行了。只需要树状数组，复杂度 $\mathcal O(n\log n)$。
3.21
CF2068K Amusement Park Rides
很神秘的题。首先题意是求是一个匹配。
维护 $M(i)$ 表示右侧点的边集。初始令 $M(a_i)={i}$，每次不断找到最小的非空的 $M(i)$，连边 $j\in M(i),(j,i)$ 和 $(i,T)$。若能增大流量，则令所有 $j\vert i,j\in \mathbb P$，在 $M(i+j)$ 中加入 $M(i)$。可以证明复杂度是 $\mathcal O(n^2\log n)$。
CF2062G Permutation Factory
下标和 $p$ 之差取 $\min$ 可以看成任选一种移动方式来移动平面上的点。感性理解一下，可以看成花费 $k$ 的代价，移动一共 $2k$ 的距离。求出最小权完美匹配之后，不断贪心移动，移动之后看一下代价和对不对就行了。
CF1852E Rivalries
CF1630F Making It Bipartite
容易发现合法的充要条件是不存在一个点同时存在因数和倍数。必要性显然，若 $x\vert y,y\vert z$ 则 $x\vert z$，这样就形成了一个三元环。充分性的话考虑如果每个点要么只有因数，要么只有倍数，那一个环上，一定是这两种点交错的，所以一定不存在奇环。
然后考虑拆点，一个点拆成倍数点和因数点，分别设为 $x_0,x_1$，表示一个点只能作为别人的倍数，或者只能作为别人的因数。然后如果 $x\vert y$，两者的合法存在方式是，$(x_0),(x_1),(y_0),(y_1),(x_0,y_1)$。
所以这样就是，$x_0$ 连边 $x_1$，$x_0$ 连边 $y_0$，$x_1$ 连边 $y_0,y_1$，求出这个图的最大独立集即为答案。
但是很遗憾，上面这个图并不是二分图，最大独立集不可求。考虑如果存在一个定向，把图定成一个偏序图（即若存在边 $x\rightarrow y,y\rightarrow z$，则存在边 $x\rightarrow z$），这个图的最长反链也就是最大独立集。可以定向为：对于每个 $x$ 连 $x_1\rightarrow x_0$ 以及对于每个 $x\vert y$ 连 $x_0\rightarrow y_0,x_1\rightarrow y_1,x_1\rightarrow y_0$。这个图的最长反链即为答案，dilworth 定理得最长反链即为最小链覆盖，dinic 跑最小链覆盖即可。
CF1693F I Might Be Wrong
I Must Be Wrong.
猜测不到只会操作 $c_0=c_1$ 的区间。不会证明：对于一次操作，假设操作区间中 $0$ 的个数大于 $1$ 的个数（否则可以 rev 再 flip，等价）。
画出折线图，$0$ 就是向右上走，$1$ 就是向右下走。如果第一个字符是 $0$ 那显然可以不操作他来减少代价，所以不断找到第一个 $1$ 的位置 $p$，找到他后面最后一个和他齐平的位置，操作这段区间。如果找不到，则一定有 $p>c_0-c_1$，此时可以加入 $p-(c_0-c_1)$ 个前缀，一次操作到最后就行了。不断重复这段过程，显然 $p$ 每次会增加至少 $1$，所以不劣。
这样按照上面的这个对整个序列贪心即可。
CF1684G Euclid Guess
首先如果 $3a_i\leq m$，可以直接构造一个 $(2a_i,3a_i)$ 的数对。
否则考虑构造一个 $(x+a_i,x)$，考虑其变化：$(x+a_i,x)\rightarrow (x,a_i)\rightarrow (a_i,x\bmod a_i)\dots$
看不出来什么？考虑再展开一步。令 $x\bmod a_i=y$。则可以构造 $x=y+a_i$，数对即为 $(y+2a_i,y+a_i)\rightarrow (y+a_i,a_i)\rightarrow(a_i,y)\dots$ 注意到可以令 $y$ 为 $a_i$ 的一个因数，这样只会加入 $a_i$ 和 $y$。而 $2a_i+y\leq m$，有 $y\leq \frac{1 }{3}m$。所以这构成了一个二分图，求出匹配即可。
3.24
[ARC195E] Random Tree Distance
流汗了，咋做过类似的还不会。
设 $f_u$ 为 $u$ 的期望深度，这个可以线性求。对于 $E(f_{\text{lca}(u,>u)})$，把 $u$ 和 $v$ 不断把深的那个向上跳。考虑 $v$ 第一次跳到 $\leq u$ 的位置，这个可以看成在 $[1,u]$ 里均匀随机。所以 $E(f_{\text{lca}(u,>u)})$ 和 $v$ 无关。
所以设 $g_u$ 表示 $E(f_{\text{lca}(u,>u)})$，有 $g_u=\frac 1 u(f_u+\sum_{i<u}g_i)$。
CF2089D Conditional Operators
jiangly 说这种题要打表。
令 $n$ 为序列长度。首先判掉 $n=3$，然后对于 $n\geq 5$，有解的充要条件是，$a_n=1$ 或者存在 $i<j,a_i=a_j=1$ 满足 $i$ 是奇数，$j$ 是偶数。对于 $n=5$ 可以验证出上述结论是对的。对于 $n>5$，考虑归纳构造。
对序列最后三个字符分类讨论。发现 $001,011,110,111$ 都满足把这三个合并之后是 $1$，那就可以直接合并。$000$ 和 $100$，这两个 $a_n\not=1$，所以前面一定存在上述满足条件的 $i,j$，容易发现直接合并也不会影响这个 $i,j$。所以除了 $010$ 和 $101$，其余六种情况都可以把最后三个直接合并。
对于 $010$，他的这个 $1$ 在偶数位置上，不能简单的抹去，因为他可能是合法的唯一的一个 $j$。所以加入倒数第四个字符。如果是 $0010$，可以操作 $(001)0$，这样这个 $1$ 仍然在。如果是 $1010$，可以操作 $1(010)$，这样也能满足还有一个偶数位置的 $1$。
对于 $101$，可以直接操作 $(*10)1$，这样最后一个位置仍然是 $1$。
归纳到 $n=5$ 的时候按照谁先合并分三种情况搜一下就行了。
CF2089E Black Cat Collapse
感觉 $n\in[60,80]$ 的题从来没想出来过。
先考虑倒着做，枚举 $i$ 表示序列长度。然后就有限制是编号为 $j$ 的只能在第 $\max(1,i-(n-j))$ 次及其之后选。然后限制最紧的那些点，就是选取的点的编号前缀最大值。那基于这个 DP，设 $f_{j,x,d}$ 表示当前选了 $j$ 个点，当前前缀最大值是 $x$，当前有 $d$ 个点确定了他要放在后面但是还没有放的方案数。$d$ 这一维是因为，从 $i$ 转移到 $j$ 的时候，需要钦定 $(i,j)$ 之间的点是否在以后加入。预处理 $trans_{x,y,k}$ 表示从 $x$ 转移到 $y$，$x,y$ 之间的点钦定 $k$ 个在以后加入的方案数。这个是一个简单的树拓扑序计数，先做一个树上背包，然后把 $(x,y)$ 这条链上挂的子树拼起来即可。
上述过程要 DP $n$ 次，状态数是 $\mathcal O(n^3)$，转移是 $\mathcal O(n^2)$，卷积可以拉格朗日插值优化到 $\mathcal O(n)$。这样复杂度是 $\mathcal O(n^5)$，应该可以过。
注意上述过程，从 $f_{j,x,d}$ 转移到 $f_{j+1,y,\ast}$ 的时候，对 $y$ 的限制是 $y\leq n-(i-j)$，只和 $i-j$ 有关，所以令 $j\leftarrow i-j$。发现上述 DP 的初值是 $f_{i-1,i,0}=1$，终值是 $\sum f_{0,x,0}$，终值是一样的。所以把 DP 转置，即把转移看成一个 DAG，等价于一个起点，问他走到所有终点的方案数之和是多少，这样只需要倒过来 DP 一次，复杂度是 $\mathcal O(n^4)$。
CF1097H Mateusz and an Infinite Sequence
CF1285F Classical?
还是太有脑子了。
首先加入所有数的约数，问题变为找两个互质的数乘积最大。
暴力可以二分莫反求出和每个数互质的最大的数。
CF1284F New Year and Social Network
首先根据观察样例 Hall 定理可得答案一定是 $n-1$。因为第二个联通块中选了 $k$ 个边，左侧被覆盖了的边数显然不可能少于 $k$（点减边的连通性）。
构造可以进行归纳构造。在 T2 上剥叶子 $i$，每次在 T1 上找到 $(i,fa_i)$ 路径上第一条边，然后把这个边的两端缩起来。实际意义是一个编号的替换，如果找到的边是 $(i,x)$，那删除点 $i$，对于所有 $i$ 的邻居 $k$，加入边 $(x,k)$。T2 中则可以直接删去点 $i$。拿一个树上倍增和并查集维护上述过程即可。
CF1284G Seollal
拟阵交？？？？
3.26
P11915 [PA 2025] 瞬间传送 / Teleport
难过，我咋记得讲过，但是咋还不会。
暴力是 $\mathcal O(n^4)$，所以考虑枚举操作的两个点 $(u,v)$，维护当前答案，检查能否变大。然后两个点 $(x,y)$ 不合法的条件是 $d(x,y)\geq ans$ 并且 $\min(d(x,u),d(x,v))+\min(d(y,u),d(y,v))\geq ans$。枚举 $x$ 之后，$y$ 是需要一个求交，复杂度是 $\mathcal O(n^4/w)$。
假设加的边是单向的，即只能从 $u$ 走到 $v$，从大到小枚举答案，每次加入不合法的 $d(x,y)>ans$ 的点对 $(x,y)$。可以实时维护 $f_{x,v}$ 表示对于已经加入的所有点对 $(x,y)$ 的 $\max(d(y,v))$。枚举 $x$，然后枚举 $v$。把所有的 $u$ 到 $x$ 按照距离从大到小排序，维护一个指针 $p_{x,v}$，每次删掉不合法的 $(u,v)$ 即可。
现在是双向的。但是如果 $d(x,y)>ans$，并且选了 $d(x,u)+d(v,y)\leq ans$，则一定有 $d(x,u)<d(x,v)$。因此考虑 $x,v$ 的时候，钦定他只能叉掉 $d(x,u)<d(x,v)$ 的所有 $u$。
P11927 [PA 2025] 重金属 / Heavy Metal
我怎么完蛋了。
meet in the meddle。$f_{i,j}$ 表示从起点走到 $i$，值为 $j$ 是否可行。然后从终点向前走，是 $g_{i,j}$ 表示当前边的乘积是 $j$，然后前面能拼的最大的一个数是多少。第二维只需要保留到根号级别，$g$ 的转移需要一个 dij，平衡到 $\mathcal O(n\sqrt{P\log n})$。
P11930 [PA 2025] 吃树叶 / Liście
操作是维护 $b$ 序列，支持前缀加，查询前缀内 $a_i$ 大于等于 $x$ 的位置 $b_i$ 的和。
操作强于行加列求和，显然得根号。暴力的单根号很简单，看其他题解吧。考虑 $nmz\leq 10^{16}$ 怎么用，我们希望能编一个 $\mathcal O(\sqrt{nmz})$ 的东西出来。
操作分块，每 $B$ 个修改操作分一块。这样一共会分成 $m/B$ 块。处理到第 $i$ 块的时候，需要计算 $[1,i-1]$ 的块对这之中的询问的贡献，以及第 $i$ 块内部的修改对询问的贡献。
$[1,i-1]$ 块的贡献
计算出 $f_j$ 表示处理了 $[1,i-1]$ 的块内的所有修改，此时 $j$ 的权值，这部分复杂度是 $\mathcal O(nm/B)$。查询就是一个二维数点。
总的修改次数是 $\mathcal O(nm/B)$ 级别的，而查询数只有 $z$。考虑平衡一下复杂度。
因为 $z$ 也是 $10^6$，常规分块复杂度还是有点高。所以可以分三层的块：设 $T=100$，每 $T$ 个位置分一个小块，这样一共有 $10^4$ 个小块。然后每 $T$ 个小块建立一个大块。维护每个点的值，小块内部的和，和大块内部的和，修改是 $\mathcal O(1)$，查询 $\mathcal O(T)$。
块内的贡献
一个修改操作 $(p_i,w_i)$ 对一个查询操作 $(q_j,d_j)$ 的贡献是 $[1,\min(p_i,q_j)]$ 内，$a$ 大于等于 $d_j$ 的点数 $\times w_i$，也就是 $zB$ 次数点，总点数是 $n$。这部分也是和上面一样的三层分块，只不过维护的是块内前缀和，大块内的小块前缀和，大块前缀和。修改 $\mathcal O(T)$，查询 $\mathcal O(1)$。
总复杂度是 $\mathcal O(nm/B+zT+zB+nT)$，取 $B=\sqrt{nm/z}$ 可以得到复杂度是 $\mathcal O(\sqrt{nmz}+(n+z)T)$。
CF1770H Koxia, Mahiru and Winter Festival
在最外层找两个匹配，然后剩下的往里缩就行了。
CF1815F OH NO1 (-2-3-4)
注意到可以构造一个环对三个点的贡献是 $5,4,3/5/7$ 和 $5,5,2/4/6$ 的情况。假设一个点在 $A$ 个环的第一个点，$B$ 个环的第二个点，$C$ 个环的第三个点，从前向后填，每次只考虑已经填了的和他相邻的点，和他相邻的点有 $B+2C$ 个。但是他的选择可以有 $2B+3C$ 种，所以一定是够的。
4.7
CF2084G2 Wish Upon a Satellite (Hard Version)
首先可以归纳证明（打表），$f(l,r)$ 在 $r-l+1$ 是偶数是，答案是 $\max(l,r)$，否则是 $\min(l,r)$。转化一下式子可以变成 $\sum_{i\leq n}i^2-\sum_{i}\sum_{j}[i\bmod 2\not=j\bmod 2]\lvert i-j\rvert$。
值域从小到大填数 DP，然后显然是凸的，平衡树维护一下就行了。
[ARC196D] Roadway
如果只有 $S<T$，限制是区间之间要么不交，要么严格包含（包含的不能在端点处相交）。加入 $S>T$ 的只有，还是要求包含的端点不交，并且对于 $S<T$ 和 $S>T$ 的内部每个区间，要么包含要么不交。这个是充要的。然后线段树简单维护即可。
P12031 [USACO25OPEN] Forklift Certified P
第一问是主席树优化建图之后求拓扑序。第二问是一个矩形最小值。
P12032 [USACO25OPEN] Lazy Sort P
首先感受一下，如果大的传向小的之后，就很难恢复了。定义势能 $\varPhi=\sum_{i}a_i^2$，显然初始和最终的势能是一样的。并且操作 $x>y$ 变成 $x-1,y+1$ 势能一定不降。所以得出结论：操作的相邻两个位置一定需要相差 $1$。
然后基于这个 DP 就行了。
P12033 [USACO25OPEN] Package Pickup P
感觉不难但是我没有一眼秒，怎么回事呢。
考虑盒子和牛的数量都是 $10^5$ 级别怎么做。一个牛一定收集他包含的一个区间的盒子，并且一定是先往左再往右。首先从前向后 DP，状态只有 $\mathcal O(1)$ 种。
对上面这个 DDP，线段树维护矩乘链，修改是单点修改，查询后做一个快速幂即可。
4.9
CF1153F Serval and Bonus Problem
比较菜。算一个积分，做二项式反演。
但是发现了一个关于二项式反演的恒等式，以前好像没正式见过：
\[\begin{aligned} f(n)&=\sum_{m\geq n}\binom m n g(m)\\ g(n)&=\sum_{m\geq n}\binom m n (-1)^{m-n}f(m)\\ \sum_{n\geq k}g(n)&=\sum_{n\geq k}\sum_{m\geq n}\binom m n (-1)^{m-n}f(m)\\ &=\sum_{m\geq k}\sum_{0\leq n\leq m-k}\binom m n (-1)^{n}f(m)\\ &=\sum_{m\geq k}\sum_{n \leq m-k}\binom {n-m-1} nf(m)\\ &=\sum_{m\geq k}\binom {m-k-m-1+1}{m-k}f(m)\\ &=\sum_{m\geq k}\binom {-k}{m-k}f(m)\\ &=\sum_{m\geq k}(-1)^{m-k}\binom {m-k+k-1}{m-k}f(m)\\ &=\sum_{m\geq k}(-1)^{m-k}\binom {m-1}{m-k}f(m)\\ \end{aligned}\]CF1097F Alex and a TV Show
对于操作 $3$ 有：
\[x(n)=\sum_{n\vert d}\mu(\frac{d}{n})\sum_{d\vert i}y(i)\sum_{d\vert j}z(j)\]令 $Y(i)=\sum_{i\vert d}y(d)$，$Z(i)$ 同理，可得：
\[x(n)=\sum_{n\vert d}\mu(\frac{d}{n})Y(d)Z(d)\\ X(m)=\sum_{m\vert n}\sum_{n\vert d}\mu(\frac{d}{n})Y(d)Z(d)\\ X(m)=Y(m)Z(m)\\\]维护这个即可。查询可以预处理之后一个 and。
CF1205E Expected Value Again
不会周期！
拆贡献，枚举 $i<j<n-1$，钦定他们都是 $n$ 的周期。可以推出实际的等价类个数是 $\max((i,j),i+j-n)$。然后拆开乱算一算就行了。
CF1085G Beautiful Matrix
比较菜，不说了。错排可以递推。
CF708E Student’s Camp
讲过。
QOJ8047 DFS Order 4
牛逼题。
一棵树的要求是儿子编号大于父亲，一个树还能唯一确定一个 DFS 序，所以考虑对所有树的 DFS 序进行去重。具体限制就是对于 $u$ 相邻的两个儿子 $x,y，(x<y)$，要求 $y$ 小于 $x$ 最大的儿子的编号，否则就可以把 $y$ 拼到 $x$ 的子树上。容易发现这个条件保证了不重不漏。
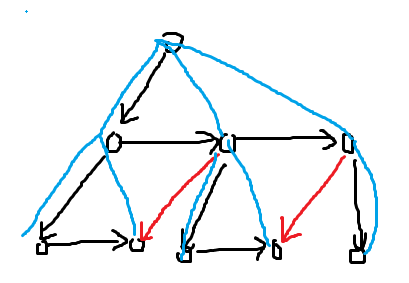
蓝色是原树结构，$u$ 指向 $v$ 的意思是要求 $v>u$，黑色是正常的限制，红色是为了去重而加上的限制。下文称蓝色的是原树，红色和黑色的结构是箭头树。我们要做的就是对所有原树的箭头树结构进行拓扑序计数并求和。
树的拓扑序计数是简单的（$\frac{n!}{\prod siz}$）。直接做显然很困难，考虑对红色的边进行容斥，用任意减去反向的。注意到反向了之后，可以变成真正树形的结构，所以这么做是对的。
$f_{i,j}$ 表示，当前子树大小是 $i$，但是根的 $siz$ 还没有确定因此还不能乘上 $\frac{1}{i}$，$j$ 的意义是根的最后一个儿子后面拼了一个子树，大小为 $j$，并且这个大小为 $j$ 的东西还没有计算贡献。
这个 $j$ 存在的意义是，因为红色边会有钦定他是反向的时刻，这样就是根的最后一个儿子的 $siz$ 以后可能会凭空变大，这样会影响箭头树整个根链。所以这个 $j$ 就是用来以后拼上去子树的时候方便处理对 $i$ 的影响的。
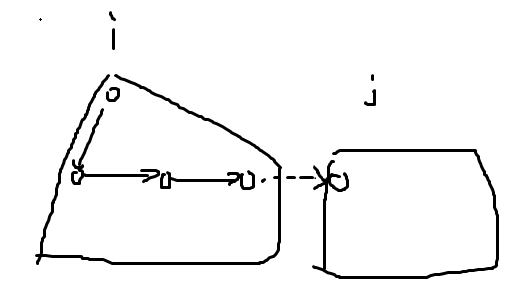
初值 $f_{i,j}=f_{i-1,0}$，表示当前根上长了一个父亲。转移：
\[f_{i,j}=\sum_{k=2}^{i-2}(f_{k,0}-f_{k,i-1-k+j})f_{i-k,j}\]意思是原树中，根的最左侧是一个大小为 $k$ 的子树。
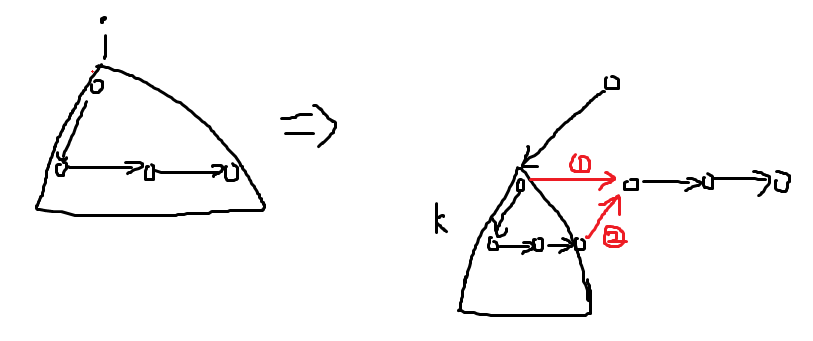
如果断掉那就是添加了 $1$ 号边，如果反向那就是加入了 $2$ 号边。（这里就体现了上文中 $j$ 的作用了，这个大小为 $k$ 的子树的根的最后一个儿子凭空出现了一个大小为 $i-1+j$ 的子树。）
转移完了之后 $f_{i,j}$ 自乘 $\frac{1}{i+j-1}$，意思是除上根的第一个儿子的子树大小。最终答案就是 $f_{n,0}(n-1)!$。$(n-1)!$ 而不是 $n!$ 的原因是根的子树大小还没有除。
复杂度 $\mathcal O(n^3)$，远远跑不满。
CF1292F Nora’s Toy Boxes
比较菜。
首先肯定只会选 $\leq 20$ 的 $a_i$，同时若 $i\vert j$，则连边 $i,j$，那么只会选入度为 $0$ 的点作为 $a_i$。这样能选的 $a_i$ 就只有 $10$ 种了。
对于每个弱连通块分别考虑。入度为 $0$ 的点显然删不掉，入度不为 $0$ 的点，考虑倒着加点，容易发现可以删到只剩一个。
对上述过程 DP：$f_{S,i}$ 表示可用的 $a_i$ 是 $S$，同时还有 $i$ 个点加入了之后 $S$ 也不会发生变化。转移是简单的。复杂度 $\mathcal O(2^Tn^2)$，其中 $T\leq 10$。
4.11
CF1948G MST with Matching
挺有意思。
树上匹配的优美性质是：把树黑白染色，最大匹配个数即为黑色点数和白色点数的较小值。这个我是通过转最大独立集之后想到的。
所以 $2^n$ 枚举每个点的颜色，只保留黑白点间的连边跑 MST 就行了。
原来我在胡扯。Accepted_100 给出了反例。
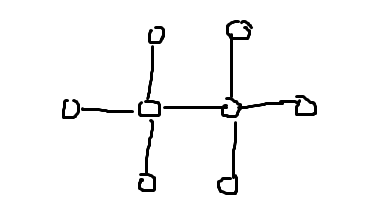
正确的方式是枚举最小点覆盖。删去两个白点间的边跑 MST。
LOJ4856 [POI 2021/2022 R3] Głosowanie
太困难。首先先手必胜。简单的对子树归纳证明即可：先任意操作一个子树。然后如果 Bob 操作了先前没有操作过的子树，那这个子树就让给他，自己去操作另一个子树。因为总数是奇数所以一定能找到另一个。而如果 Bob 操作了之前 Alice 操作过的子树，根据归纳假设这个子树里 Alice 能赢，所以 Alice 继续在这个子树里操作一步还是能保证他必赢的。
基于这个维护即可。稍微转化一下。首先 Alice 任选一个叶子，然后 Bob 选了一个。找到 Bob 本次选的根链和 Alice 先前选的所有点构成的虚树，两者的第一个交点此时一定有偶数的度数，Alice 操作另一个儿子即可。
LOJ4857 [POI 2021/2022 R3] Rzeki
不大懂。本质不同的间隔只有根号种，然后拿值域分块乱维护就是单根号的。
CF1737F Ela and Prime GCD
神秘构造题。不大会做。
CF1737G Ela Takes Dancing Class
比较菜啊。首先如果 $d>a_n-a_1-n$，则每次都是最前面的移动到最后面，形成了一个循环了。
所以从前到后考虑每一个人，维护当前的循环节 $[1,i]$。每次找什么时候跳到了 $i+1$ 这个人的后面，则 $i+1$ 就加入了循环节。拿平衡树维护循环移位即可，感觉不大好写。
CF1696H Maximum Product?
烂炸了。不想说了。
4.14
QOJ10333 Divide Digit String
首先 $k>1$ 是简单的，答案一定是个位数，枚举答案之后随便贪心一下即可。
对于 $k=1$，答案的位数一定是 $\lceil \frac n m \rceil$，所以可能的答案串只有 $n-m$ 个。后缀排序之后二分答案，每次贪心往后拼一段尽可能长的即可。
QOJ10327 Convex Hull of Intersections
神秘题。首先考虑若斜率互不相同，考虑枚举所有方向，找到这个方向上的第一个点，所有方向的点的集合即为凸包。
考虑若在无限远处做一条直线，题目给的所有直线在这根直线上的交点，相邻的两个交点一定属于斜率相邻的两条直线。而把无限远的这条直线逐渐拉近，其他直线和这根直线的交点会移动，当两个交点重合的时候，就出现了题给两个直线的交点。所以一定只有相邻两个交点才可能最先合并。
所以斜率互不相同时，按照斜率排序，加入相邻斜率的直线的交点求凸包即可。
对于有斜率相同的，显然只需要保留两条，然后做和上面一样的操作即可。
QOJ10331 Shuffle and Max Bracket Score
讲过。这里 D18T3。
QOJ10324 Swap Counter
交换 $i$ 和 $i+1$ 时，把这次交换归为 $i+1$。那一个点就会从 $i$ 走到 $i-c_i$，$c_i$ 表示 $j\in [1,i-1]$，$a_j>a_i$ 的个数。相当于 $[i-c_i,i)$ 区间加一。因为右端点确定了，所以根据差分值可以确定所有 $i-c_i$ 的集合。
现在要求字典序最小。考虑 $i-c_i-1$ 的意义是 $[1,i-1]$ 中比 $i$ 小的数的集合。考虑从小到大加入 $i-c_i-1$。第一次加入的是 $=0$ 的，这些数是前缀最小值。然后加入等于 $1$ 的时候，加在第一个和第二个之间。$=2$ 的加在第二个和第三个之间。
QOJ10322 Matching Query
好难。
首先求出相邻两个数 $i,i+1$ 的最大匹配 $b_i$，第 $i$ 个数的出现次数为 $a_i$，问题变为确定一组 $x$，使得 $x_i\leq b_i$ 并且 $x_i+x_{i+1}\leq a_i$，最大化 $\sum x$。
最大匹配 $b$ 是简单的，看成一个括号序列，左括号加一，右括号减一，对于每个 $i$ 开一棵线段树维护求前缀最小值即可。
后面这个怎么求呢？可以证明（？？）可以看成线性规划求出答案之后下取整，同时求出的答案一定是 $0.5$ 的倍数。
哎扔了。不会。
QOJ10330 Median Operations
显然要 $01$ 染色。然后稍微推一下发现 $010$ 的时候把两边的 $0$ 并起来是优的，但是一旦出现两个 $1$ 就不优了。随便线段树维护即可。
QOJ10323 2-Power Rush
列一下 GF：
\[F(x)=\prod_{i\geq 0}\frac{1}{1-2^ix^{2^i}}\]式子比较丑陋。我们希望提取出 $x^{2^i}$ 前面的所有系数，显然就是 $\sum_{j\leq i}2^{j2^{i-j}}$。
然后就可以数位 DP 了。暴力是 $\log^3 V$ 的，但是可以折半优化到 $\mathcal O(T\log V+\sqrt V \log^2 V)$。具体来说，前一半的位预处理所有情况对应的 DP 值，后一半的位预处理转置 DP 所有情况对应的值，查询就是枚举中间状态把两边拼起来。
4.21
CF2096F Wonderful Impostors
合法的条件是，不存在一个 $1$ 区间全部被 $0$ 区间覆盖。然后答案还具有单调性，所以可以双指针。
然后随便维护一下就行了。先维护每个位置被 $0$ 覆盖的次数，然后每个位置，维护 $nex_i$ 表示，以这个点为起点，$1$ 区间最小的右端点。然后合并的时候随便分类讨论一下。
CF2096G Wonderful Guessing Game
非常困难。
首先如果不会忽略答案，答案下界是 $\lceil\frac n 3\rceil$。事实上能取到。
$a_{i,j}$ 表示第 $i$ 次询问。则对于每两列需要他们有至少一个不一样的位置，并且每一行中 $L$ 和 $R$ 的数量相等。
这是容易构造的，令 $t=\lceil\frac n 3\rceil$，取出 $(0,3^t)$ 之间的所有数，每一列都选一个数，如果第 $i$ 位是 $0$ 则对应 $N$，$1$ 则对应 $L$，$2$ 则对应 $R$。如果 $n$ 是偶数，可以每次取一个还没取的数 $x$，然后取一个数 $y$ 满足，如果 $x[i]=1$ 则 $y[i]=2$，如果 $x[i]=2$ 则 $y[i]=1$，如果 $x[i]=0$ 则 $y[i]=0$，这样可以满足每一行中 $L,R$ 的数量相等。
对于会忽略一次询问，答案下界是 $\lceil\frac n 3\rceil+1$。事实上也能取到。只需要多加一行，然后令每一列中，$L+2R$ 的和 $\bmod 3$ 是 $0$，这样就算丢了一行也能确定其余所有的。
CF2096H Wonderful XOR Problem
还不大会。一个子问题是求 $\prod (a_ix^{b_i}+c_ix^{d_i})$，乘法是异或卷积。
首先对于 $b,d$ 都相同的一对数，令 $a’=(a_1a_2+c_1c_2),c’=(a_1c_2+a_2c_1)$ 就能把它们合并。然后问题就变成了 $\prod_i a_i+b_ix^i$。我们可以求出 $ans_j=\sum_{j}[x^i]\text{FWT}(a_i+b_ix^i)$，最后再 IFWT 回去就行了。显然有：
\[[x^j]\text{FWT}(a_i+b_ix^i)=\begin{cases} a_i+b_i\;\;\;\;\;\;\;\;\;\;\text{popcnt(i\&j)}\bmod 2=0\\ a_i-b_i\;\;\;\;\;\;\;\;\;\;\text{popcnt(i\&j)}\bmod 2=1\\ \end{cases}\]然后类似的做 FWT 即可。设 $f_{i,0}$ 表示真实答案，$f_{i,1}$ 表示，如果 $\text{popcnt(i\&j)}\bmod 2=0$ 则算入 $a_i-b_i$ 的贡献，否则算入 $a_i+b_i$ 的贡献（也就是反着算）。初始 $f_{i,0}=a_i+b_i,f_{i,1}=a_i-b_i$。考虑到第 $t$ 位时，对于所有 $i[t]=0$，$j=i\oplus 2^t$ 执行：
\[f'_{i,0}=f_{i,0}f_{j,0}\\ f'_{i,1}=f_{i,1}f_{j,1}\\ f'_{j,0}=f_{j,1}f_{i,0}\\ f'_{j,1}=f_{j,0}f_{i,1}\\\]最后 $ans_i=f_{i,0}$，然后做 IFWT 就行了。
ARC072A Rhythm Game
我是傻逼。
问题可以看成，第 $i$ 个任务是，从 $t_i-x_i$ 时刻开始，需要工作 $2x_i$ 的时间，截止时间是 $x_i+t_i+D$。首先如果所有工作都开始了，按照截止时间从小到大工作一定是最优的。假设工作时长是 $c_i$，截止时间是 $d_i$，可以邻项交换证明：
\[min(d_1-c_1,d_2-c_2-c_1)>min(d_2-c_2,d_1-c_1-c_2)\\ min(d_1+c_2,d_2)>min(d_2+c_1,d_1)\\\]因为 $d_1+c_2>d_1$，所以若 $d_2\leq d_1$，则左侧为 $d_2$，右侧的两个数都 $\geq d_2$。所以 $d_2>d_1$ 是一个必要条件。同时发现 $d_2>d_1$ 了之后右侧一定是 $d_1$，也充分了，所以充要条件就是 $d_2>d_1$。
但是现在有了发布时刻。但是按照截止时间排序，如果进行完了工作 $i$ 后直接进行工作 $j$，则进行完了工作 $j$ 之后，$(i,j)$ 之间的工作一定都发布了。这是显然的。所以进行完 $j$ 之后一定是立刻处理 $(i,j)$ 的工作。然后就可以 DP 了。可以简单优化到 $\mathcal O(n^2)$。
4.23
QOJ10514 疲配
首先考虑没有修改一条边怎么做。看成一个矩阵，第 $i$ 行第 $j$ 列有一个多项式 $x_{i,j}y_{c_{i,j}}$，要求这个矩阵的行列式。其中 $y$ 这一维是对 $y^2-y$ 取模也就是或卷积。所以可以进行 FWT，枚举一个 $[k]$ 的子集表示这里面的 $y$ 是 $1$ 其余的 $y$ 是 $0$，然后 $x_{i,j}$ 随机赋权即可。这样求完 $2^k$ 次行列式之后，最后再 IFWT 一下，所有不为 $0$ 的位置即为合法。
对于能修改一条边，看成每个位置的多项式变成 $x_{i,j}(y_{c_{i,j}}+y_{c_{i,j}-1}z+y_{c_{i,j}+1}z)$，要求这个矩阵行列式中 $[z^0]$ 和 $[z^1]$ 的值。那如何求 $\text{det}(A+Bz)$ 呢？拉插是平凡的，但是其实也可以直接暴力：每次找到这一行上 $a$ 不为 $0$ 的位置来当做朱元，因为 $\bmod z^2$ 意义下只要常数项不为 $0$ 就是有逆的。如果 $a$ 全为 $0$，那这一行整体除 $z$，如果还全为 $0$ 就死了，否则就能正常消了，复杂度是 $\mathcal O(n^32^k)$。
还可以在 $\mathcal O((nk)^3)$ 的复杂度内求 $\text{det}(A_0+A_1z+A_2z^2+\dots+A_kz^k)$。首先可以化简为 $\text{det}(Iz^k-A_0-A_1z-A_2z^2-\dots-A_{k-1}z^{k-1})$。
首先有：
\[\begin{vmatrix} A&B\\ C&D \end{vmatrix}= \begin{vmatrix}A\end{vmatrix}\begin{vmatrix}D-CA^{-1}B\end{vmatrix}\]考虑矩阵：
\[\begin{bmatrix} 0 & \mathbf{I} & & & \\ 0 & 0 & \mathbf{I} & & \\ \vdots & \vdots & \ddots & \ddots & \\ 0 & 0 & \cdots & 0 & \mathbf{I} \\ \mathbf{A}_0 & \mathbf{A}_{1} & \cdots & \mathbf{A}_2 & \mathbf{F}_1 \end{bmatrix}\]