DS
P6109 [Ynoi2009] rprmq1
现在看其实还好。
最大值查询很烦,不能差分,分治一下就好了。
P8512 [Ynoi Easy Round 2021] TEST_152
从前向后扫,维护序列颜色段,每个段有两个属性:颜色和权值。要查询的是颜色大于等于 $x$ 的权值和,再开一个树状数组维护这个就行了。
P8337 [Ynoi2004] rsxc
从左向右扫,求出每个位置的序列线性基,要求就是如果有 $k$ 个基底,则要求颜色数是 $2^k$,这样求出了 $\mathcal O(n\log n)$ 个区间。然后要查历史和状物。暴力做很不牛。
考虑对于一个 $k$,区间的左右端点都是单调的。所以预处理之后可以 $\mathcal O(1)$ 查询。
P8265 [Ynoi Easy Round 2020] TEST_63
LCT,让虚实边对应轻重边。
修改只会修改不超过 $\mathcal O(\log n)$ 个点的重儿子。link 和 cut 的时候暴力跳检查一下是否需要改儿子就行了。对于换根,可以维护最大轻儿子减重儿子的大小,复杂度大概是对的(?)。
P6780 [Ynoi2009] pmrllcsrms
按照 $c$ 定长分块,不跨过边界的是好处理的。
对于跨过边界的,是一个三角形查询状物。
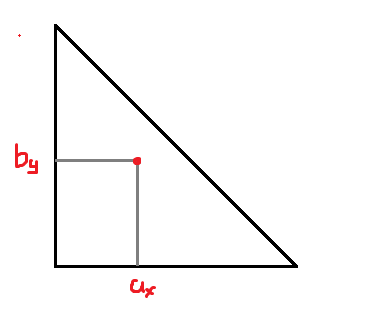
考虑在这个上面建线段树!分治!
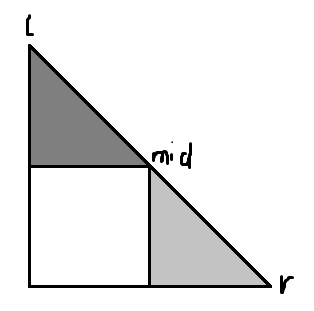
矩形的答案可以通过两侧的三角形算出来,这样就可以合并了,总复杂度也是一个 $\log$。
P6105 [Ynoi2010] y-fast trie
首先所有数要先 $\bmod C$。对于 $(x+y)-C$ 的话,是取两个最大值。
对于 $x+y<C$ 的情况,考虑维护双向匹配的最大值。修改只会改 $\mathcal O(1)$ 个匹配。
P6018 [Ynoi2010] Fusion tree
倒着建 trie 可以做整体加一。一个点维护所有儿子形成的 trie,父亲特殊查询。然后做完了。
P8531 [Ynoi2003] 戌亥彗星
我是奶龙/dy。
一个环可以用 LCT 找出一段合法区间。一个连通块可以点减边,线段树维护。除了环以外度数不大于 $3$ 可以在 LCT 上维护度数最小值以及个数。上个历史和做完了。
数数
[AGC060C] Large Heap
汗流浃背了吧。
考虑把这棵树最左和最右的两条根链进行归并,这样限制就是 $u$ 需要在 $v$ 的上面。归并之后仍然是一棵树,就是一个拓扑序计数。
[AGC060D] Same Descent Set
我没救啦。
考虑先枚举 $n-1$ 对相邻的大小关系,计数出这种大小关系对应的方案数 $v$ 之后,所有的 $v^2$ 求和即为答案。
如果给定了大小关系如何计数?经典容斥:枚举 $>$ 变成 $<$ 或者无限制,前者有 $-1$ 的系数,枚举了之后设极长的 $<$ 连续段的长度分别为 $l_1,l_2\dots l_k$,则方案即为 $\binom{n}{l_1,l_2\dots l_k}$。
设 $f(S)$ 表示枚举了 $S$ 中的位置是端点,其余位置全都是 $<$ 号的方案数。答案即为:
\[\begin{aligned} &\sum_{S\subseteq [n-1]}(\sum_{T\subseteq S}(-1)^{\lvert S\rvert-\lvert T\rvert}f(T))^2\\ =&\sum_{S\subseteq [n-1]}(\sum_{A\subseteq S}(-1)^{\lvert A\rvert}f(A))(\sum_{B\subseteq S}(-1)^{\lvert B\rvert}f(B))\\ =&\sum_{A\subseteq [n-1]}(-1)^{\lvert A\rvert}f(A)\sum_{B\subseteq [n-1]}(-1)^{\lvert B\rvert}f(B)2^{n-1-\vert A\rvert-\lvert B\rvert+\lvert A\cap B\rvert}\\ =&2^{n+1}\sum_{A\subseteq [n-1]}(-\frac{1}{2})^{\lvert A\rvert+1}f(A)\sum_{B\subseteq [n-1]}(-\frac 1 2)^{\lvert B\rvert+1}f(B)2^{\lvert A\cap B\rvert} \end{aligned}\]最后一个 $2^{\lvert A\cap B\rvert}$,考虑组合意义,就是对于 $A,B$ 都存在的断点,可以“选”他,也可以不“选”他,对所有“选”法求和。
所以先枚举若干段 $A$ 拼成长度为 $k$,然后若干段 $B$ 拼成长度为 $k$,令这个方案数为 $f_k$,最后就是要再枚举若干段 $f_k$ 求和(就是上述“选”带来的贡献,如果“选”了那就在此处合并,如果没“选”就在第一步拼成 $f_k$ 的时候合并)。
一个连续段的 GF 是:
\[F=\sum_{i\geq 1}\frac{x^i}{i!}\]注意这里的 $x_i$ 指的是序列长度为 $i$,而不是有 $i$ 个间隔。拼成一个长度为 $k$ 的断 GF:
\[G=\frac{1}{1+\frac{1}{2}F}\]然后令 $H=\sum_{i\geq 0}g_i^2x^i$,求出 $\frac{1}{1-H}$ 即可求出答案。