My Blogs
[ARC171E] Rookhopper’s Tour
因为每行每列都最多只有一个石子,所以一定是横竖相间的走。
首先手玩一下,可以发现白色石子放置好了之后,最多只有一种合法的走法,因为确定了第一步走的方向,后面由于题目中没有行列相同的白石子,所以之后的路线是唯一的。所以算重只需要考虑把路线反过来还能走。然后画一下图就可以发现显然不合法(可能严谨一点的需要归纳)。
然后是一个非常妙的想法。先不管最后要回到起点,考虑任意一条路径,做边走边放棋子的过程。考虑从 $(x,y)$ 越过石子 $(x,t),t>y$ 走到 $(x,t+1)$,就增加了限制:以后的石子不能放在 $x$ 行和 $t$ 列。
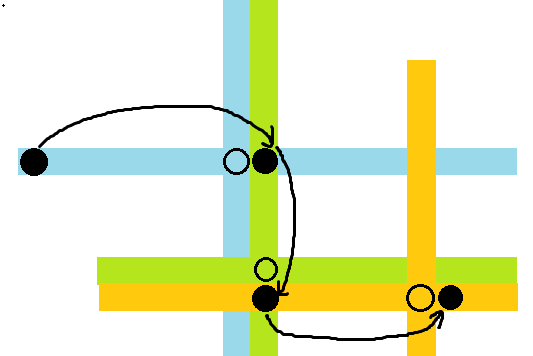
蓝色,绿色和橙色分别表示三次跳跃的新添限制。然后可以很深刻的发现,相邻的两个限制是可以合并的,即此时在 $t+1$ 列一定还有一个石子,所以限制可以改为不能放在 $x$ 行,$t,t+1$ 列。
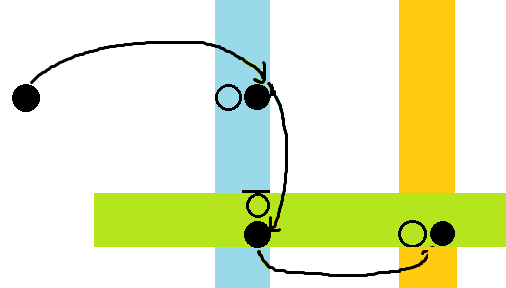
这样就可以对行和列分开做了。然后考虑加上需要回到 $1$ 的限制,假设第一步是上下走的,则倒数第二步一定是走回和 $(a,b)$ 在同一行的点,最后一步一定也在 $a$ 这一行。所以枚举它第一步走的是上下还是左右,假设是上下,然后枚举倒数第二步是从上面走到 $a$ 行还是从下面走到 $a$ 行,从左边还是右边回来。
这样可以转化为计算 $\mathcal O(1)$ 次如下问题:给定 $a,b,c,d,m$,对长度为 $a$ 的序列进行 $i$ 次染色,对长度为 $c$ 的序列进行 $\frac m 2 -1-i$ 次染色,每次染色要求涂黑相邻两个黑色格子,并且黑色格子之间不能重叠。对长度为 $b,d$ 的序列,在 $b$ 中染 $j$ 次,在 $d$ 中染 $\frac m 2-1-j$ 次,这样一个方案的权值就是 $ij((m-1)!)^2$。$i,j$ 是在选倒数第二次和最后一次走到了哪个黑色对,$(m-1)!$ 是剩下的可以任意选择顺序走。
使用插板法,在 $a$ 中填了 $i$ 个黑色对,还剩下 $a-2i$ 个白色对,这些白色对把序列分成了 $a-2i+1$ 个间隔,方案数即为 $\binom{a-2i+1+i}{i}$。对于剩下的序列都可以类似计算,总复杂度 $\mathcal O(n+m)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int n,m,A,B,ans,fr[400010],inv[400010];
inline int C(int n,int m){return m<0||m>n?0:Cmul(fr[n],inv[m],inv[n-m]);}
inline void calc(int x,int y,int z,int t)
{
int L=0,R=0;
for(int i=1;i<=m;++i)Madd(L,Cmul(i,C(x-2*i+i,i),C(z-2*(m-i)+(m-i),m-i)));
for(int i=1;i<=m;++i)Madd(R,Cmul(i,C(y-2*i+i,i),C(t-2*(m-i)+(m-i),m-i)));
Madd(ans,Cmul(L,R));
}
inline void mian()
{
read(n,m,A,B),fr[0]=inv[0]=1;
if(m&1)return write(0);m>>=1,--m;
for(int i=1;i<=400000;++i)fr[i]=Cmul(fr[i-1],i);
inv[400000]=power(fr[400000],MOD-2);
for(int i=399999;i>0;--i)inv[i]=Cmul(inv[i+1],i+1);
calc(n-A-1,n-B-1,A-1,B-1);
calc(n-A-1,B-2,A-1,n-B);
calc(A-2,n-B-1,n-A,B-1),calc(A-2,B-2,n-A,n-B);
write(Cmul(ans,2,fr[m-1],fr[m-1]));exit(0);
}