Day 1
T1
可以做快速幂,每次 $\times 2$ 或者 $\times 2+1$。然后从后向前考虑后面对前面的影响即可。
T2
考虑枚举出现次数 $k$,计算众数出现次数 $\geq k$ 的序列数,转成 $n^m$ 减去所有颜色出现次数都 $<k$ 的序列数。考虑一种颜色指数生成函数 $F(x)=\sum_{i<k}\frac{x^i}{i!}$,需要求这个多项式的 $m$ 次幂,多项式快速幂就行了,总复杂度 $\mathcal O(n^2\log n)$。
T3
对 $A$ 建出笛卡尔树,因为要求区间长度尽可能长,所以只保留笛卡尔树上的节点就是对的。
考虑算出每个节点什么时候变得合法。有一个很简单的做法:考虑区间或和只会变化 $\log V$ 次,并且祖先区间的或和是子孙区间的超集。这样修改的时候可以从每个点暴力网上跳,如果这个点或上了 $y$ 之后区间或和不变,就 break,否则继续向上跳。
找到合法时间点之后,询问可以维护区间长度为下标的 BIT,复杂度 $\mathcal O(n\log V+q\log n)$。
T4
| [做过]([Keep XOR Low - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)](https://www.luogu.com.cn/problem/CF1616H))。考虑设 $f_i$ 表示 $i$ 子树内任意选的最大答案。然后发现做不了,问题在于可能递归向两侧。然后有一点性质是如果递归到两侧 $f(x,y)$ 表示必须在 $x,y$ 内都选的最大值,则 $x$ 对应的路径和 $y$ 对应的路径的异或值(高于 $x$ 当前位的)一定等于限制 $k$,所以暴力做 $f(x,y)$ 递归的时候分类讨论一下复杂度就是对的。 |
然后因为修改根链只会更改 $\log$ 个点, 所以暴力记忆化搜索还是对的。
Day 2
T1
有点魔怔,打表,观察 $a_i>i$ 的位置,可以发现等价于从 $(x,y)$ 走到 $(n,n)$,中途纵坐标大于等于横坐标的方案书,可以容斥。
T2
考虑对原图拓扑排序,则 $i$ 能到达的点在 $i$ 之后。预处理 $f_i,g_i$ 表示以 $i$ 开头,结尾的最长路。然后删掉了 $i$ 之后,剩下的最长路是拓扑序在 $i$ 前的的 $g_i$ 的最大和 $i$ 之后的 $f_i$ 的最大值,还有跨过 $i$ 的一条边,贡献是 $g_u+f_v$,可以用堆简单解决。
T3
考虑如何 chk。从前向后扫,一个点如果当前不合法,则一定要为它新建一个新的维度,这样暴力 chk 一次是 $\mathcal O(nk!)$ 的。
考虑从后向前 dp。设 $f_{i,p,j}$ 表示当前在 $i$ 点,使用排列 $p$ 来新建维度(遇到第一个不合法点把 $p_1$ 维确定,然后用 $p_2$ 维…以此类推,然后第 $j$ 次新建维度遇到的点的最大值。
对于转移,如果 $a_{i,p_1}=a_{i+1,p_1}$,则 $f_{i,p}=f_{i+1,p}$。否则需要从后面找一个 $p_i$ 移动到第一位。
T4
首先把 $01$ 连续段缩起来。然后割 $k$ 次($k>1$)等价于从里面选 $k+1$ 个子序列,每个段内颜色相同,并且之间互相不交,长度和的最大值。
容易发现删掉中间一个会使 $k-2$,删掉边上的会使 $k-1$,可以分讨一下反悔贪心做。
Day 3
哎。
T1
因为颜色只有 $n$ 种,所以对每个颜色预处理 $f_{i,j}$ 表示 $(i,j)$ 需要正方形半径为 $f_{i,j}$ 时才包括一个该颜色。对于每个点桶处理一下,然后做完了,时间复杂度 $\mathcal O(n^3)$,需要一定常数优化。
T2
首先预处理 $F_{i,j}$ 表示 $i$ 结尾的长度为 $j$ 的上升子序列的数量,树状数组 $\mathcal O(n^2\log n)$ 做,然后处理出 $f_i=(n-i)!\sum_{j}F_{j,i}$。这样算出来的显然不对。
考虑容斥,对于一个操作顺序,最后剩下了一条长度为 $i$ 的链,则其对于 $f_j(j\leq i)$ 的贡献为 $(i-j)!\binom i j$。设 $g_i$ 表示实际最后长度为 $j$ 的方案数,列出关系式:
\(\begin{aligned} f_i&=\sum_{j\geq i}g_j\binom j i(j-i)!\\ &=\sum_{j\geq i}g_j\frac{j!(j-i)!}{i!(j-i)!}\\ &=\sum_{j\geq i}g_j\frac{j!}{i!} \end{aligned}\) 已知 $f$,$\mathcal O(n^2)$ 暴力从后向前反演解出 $g$ 即可。
T3
哈哈。
从前向后看起来做不了。值域从大到小想了一下好像也做不了,为什么没想到值域从下向上呢?
考虑单次,值域从小到大扫,此时可以吧这个点移到左边或者右边,移到较近的一个一定更优。所以问题变成每个点左边比他大的数的个数和右边比他大的数的个数两者取 $\min$,随便做一做。
T4
真的不懂啊。为啥不会啊。行列分开想很难吗?非得对着你那个傻逼 L 形死磕到死吗???
首先考虑确定了前 $M$ 列的所有,此时 $M$ 右边的方案数如何计算。相邻左右两个矩形可以做差分:
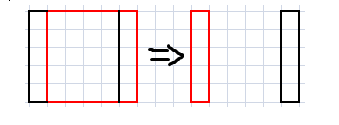
上面左边红框和黑框相等等价于右侧红框和黑框相等。然后再对这个再做一遍差分:
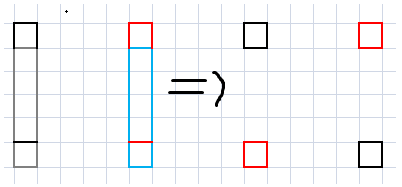
红黑相等和蓝灰相等可以推出右侧红黑相等。这样可以观察到一些性质:
- 右侧每列是独立的。能填什么只和 $(j-1)\bmod M+1$ 列的形态有关。

对矩形左右差分可以得到这个结论。
对于一列,$i\bmod N$ 同余的点也是相对独立的。

黑格子代表 $1$,白格子代表 $0$,如果像左边两张图一样,根据上面的结论,右下角应该填 $-1$ 或者 $2$,不合法,合法的只有右边两张图的情况。这样可以导出一个重要结论:$i\bmod N$ 相同的一堆点如果同时有黑白的点,则他右边的所有依赖他的点全都只能填和他一样的颜色。如果全都是黑白则可以翻转,并且对于要求每一列黑白翻转数相同。
这样一列如果有 $i$ 个全黑同余,$j$ 个全白同余,后面 $\bmod M$ 和这一列同余的点的填法的方案数就是 $\binom{i+j}{j}^{\frac{M}{m}-1}$。
对于前面的部分,做一个上下差分:

限制是蓝色的每行对应相等,橙色的每行对应相等,所以可以一行一行的填,每次把一个蓝色全填完。
可以比较暴力的做,设 $f_{i,A,B}$ 表示填了 $i$ 次,当前 $[1,M]$ $M$ 个位置,全 $0,1$ 行的个数分别为 $a_i,b_i$ 的方案数,转移就是枚举这一行填了什么,复杂度比较爆炸,大概有 $50$ 分左右。
但是可以发现,只需要记录全 $0$ 或全 $1$ 列的个数,最后再处理一下即可,设 $f_{i,S}$ 表示填了 $i$ 次,每列的全相等行的数量集合是 $S$。转移枚举一个 $2^M$ 的二进制数表示这一列的这个行组是否全相同,还是需要预处理一下转移系数,这样大概有 $80$ 分。
比较典的,不关心集合顺序,所以 $S$ 可以从小到大排序,状态数进一步减少,可以获得 $100$ 分。
Day 4
T1
$f(x)$ 显然单调递减,可以二分答案找到 $>k$ 最小的和 $<k$ 最大的。二分了答案之后可以单调队列优化 DP。
T2
首先枚举选的区间 $k$,设 $f(i,j,k)$ 表示一个长度为 $k$ 的序列,最大值
是 $i$,最小值是 $j$ 的方案数,则答案为: \(\sum_{k\geq 1}m^{n-k}(n-k+1)\sum_{i\leq j}f(i,j,k)ij\\\) $f$ 可以容斥计算: \(f(i,j,k)=\begin{cases}(j-i+1)^k-2(j-i)^k+(j-i-1)^K \;\;\; i<j\\ 1\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\quad\;\; i=j \end{cases}\) 答案即为 \(\begin{aligned} &\sum_{k\geq 1}m^{n-k}(n-k+1)\sum_{p\geq 1}(p+1)^k-2p^k+(p-1)^k\sum_{i+p\leq m}i(i+p)\\ =&\sum_{k\geq 1}m^{n-k}(n-k+1)\sum_{p\geq 1}((p+1)^k-2p^k+(p-1)^k)v(p)\\ =&\sum_{p\geq 1}v(p)\sum_{k\geq 1}m^{n-k}(n-k+1)((p+1)^k-2p^k+(p-1)^k)\\ =&m^n\sum_{p\geq 1}v(p)\sum_{k\geq 1}(n-k+1)((\frac{p+1}{m})^k-2(\frac pm)^k+(\frac{p-1}m)^k)\\ =&m^n\sum_{p\geq 1}v(p)[(n+1)(f(\frac{p+1}m)-2f(\frac p m)+f(\frac{p-1}{m}))+g(\frac {p+1}m)-2g(\frac p m)+g(\frac {p-1}m)]\\ \end{aligned}\) $\displaystyle f(v)=\sum_{i\leq n} v^i,g(v)=\sum_{i\leq n} iv^i$,两个都能 $\mathcal O(\log V)$算。
T3
首先建出来正反串的 trie 树,对于一个字符串,再 $s[1,i]$ 和 $s[i+1,n]$ 之间连边,变成找四元环。可以让度数大的指向度数小的,时间复杂度 $\mathcal O(m\sqrt m)$。
T4
首先考虑 $a_{i,1}=a_{i,2}$ 怎么做。打表(?)发现长度为偶数的序列一定是一半一半的取完,长度为奇数的序列中间的点有一个竞争,一定是 $A$ 取 $1,3,5\dots$ 大的,$B$ 取 $2,4,6\dots$ 大的。
然后如果 $a_{i,1}\not=a_{i,2}$,设 $f_{i,0/1,0/1}$ 表示选了前 $i$ 个,$i$ 选的左还是右,$i-1$ 选的左还是右的最大值。此时奇数序列对中间的数的贡献不同,如果对 $A$ 的贡献是 $a_i$,$B$ 的贡献是 $b_i$,考虑邻项交换,对于两个二元组 $(a_1,b_1)$ 和 $(a_2,b_2)$,如果 $A$ 先选了第一个二元组,则贡献是 $a_1-b_2$,否则是 $a_2-b_1$,要求 $a_1-b_2>a_2-b_1$,即 $a_1+b_1>a_2+b_2$。按照这个排序就可以做不带修的情况。
对于带修,DP 部分可以线段树优化矩阵乘法,奇数序列的中间部分只需要维护一个平衡树或者值域线段树,维护奇数和和偶数和的差即可。总复杂度 $\mathcal O(m\log nT^3)$,其中 $T=4$。
Day 5
T1
从小到大排序,答案上界是 $(a_{i+1}-a_i)\min(i,n-i)$。取到上界的方式就是把 $\leq\frac n 2$ 的和 $>\frac n 2$ 交替着放。方案数对于偶数就是 $2(\frac n 2)!$,对于奇数,$a_{\frac{n+1}2}$ 没有贡献,可以随便放,所以就是 $2(\frac n 2)!n$。
T2
对于 $A\leq B$ 的情况可以直接 bfs,到某个点就是这个点的最短时间,如果此时杀不掉那永远杀不掉。
对于 $A>B$,先判断是否能杀到 $n$:拿一个小根堆维护当前所有能接触到的,每次选堆顶杀掉,如果杀不掉 $n$ 那一定不合法。
否则找到所有上述过程中杀掉了的点,它们是最优解中能到达的点。然后算出来 $w_i$ 表示第 $i$ 个点什么时候有能力杀掉,再在原图上用一个类似 dij 的东西,每次取出最小的 $dis_i$,对周围的点进行扩展 $dis_j=\min(dis_j,\max(w_j,dis_i))$。复杂度 $\mathcal O(n\log n)$。
T3
离线询问,建出来 AC 自动机。分两种情况讨论:第一种是 $t$ 跨过回文串的中点,这种情况就是直接把 $S$ 的反串在 AC 自动机上跑,统计答案的时候判断祖先节点是否是回文即可。
| 对于 $S$ 跨过回文串中点的情况,先 manacher 预处理 $f_i$ 表示以 $i$ 结尾的回文串数量,然后还是把反串在 AC 自动机上跑,但是这次权值不是 $1$ 是 $f_{i-1}$,统计答案还是贡献给所有祖先,总复杂度 $\mathcal O( | S | \sum)$。 |
T4
好牛啊,没见过的套路。
首先转成找最大的 $i$ 满足 $\sum_j [a_j<i]\geq i$。polylog 看上去非常的不可做,暴力就是莫队加值域分块,复杂度 $\mathcal O(m\sqrt n)$。
但是它真的可以 polylog。离线所有询问,从大到小扫描值域 $i$。考虑每次判断哪些区间答案是 $i$,就把他们直接删掉。直接做还是很爆。
考虑一点性质:区间的答案一定不劣于其内部的区间。所以尝试只保留不被其他区间包含的区间,把他们挂在右端点上,这样左端点就是递增的。当 $i-1$ 的时候就可以线段树上二分再加一个区间 $-1$ 来维护区间的权值。
然后一个区间权值减到 $0$ 了如何处理。他被删去之后可能有多个区间被加入。设删掉了 $[l,r]$,其左边相邻的区间是 $[l_1,r_1]$,右边相邻的区间是 $[l_2,r_2]$。则新加入的区间 $[l’,r’]$ 需要满足 $l’<l_2$ 并且 $r’>r_1$。然后一次可能加入多个区间,就从右向左做,线段树上要维护能够加入的新区间左端点最小值。这样总复杂度 $\mathcal O(n\log n)$。
Day 6
T1
从前向后填,能填上 $i$ 的条件是当前位置后面第一个 $i$ 的位置后面出现了所有数(还未加进序列里的)。
所以拿一个可删堆维护每种颜色最后一次出现位置,然后要在前面找一个合法的最小数也可以拿一个堆维护,总复杂度 $\mathcal O(n\log n)$。
T2
设 $f_{i,j}$ 表示 $i$ 当前连通块内选了 $j$ 作为关键点的权值最大值,$g_{i,j}$ 表示 $i$ 当前连通块内没有关键点,并且深度最大的点是 $j$。转移复杂度是树形背包。
T3
并查集,树状数组维护区间哈希值,每次向后找到第一个不同的位置,复杂度均摊 $\mathcal O(n\log^2 n)$。
T4
太难了。
Day 7
T1
找到直径,对于每个点和直径两个端点加边,跑 MST 即可。
T2
枚举矩形用了几个不同的行分界线和列分界线,然后状压 DP 一下啥的。
T3
感觉比较牛。还是不太会平衡思想。
首先设 $f_{i,j}$ 表示 $i$ 点的值标的 $j$ 的方案数。转移状压 DP,复杂度 $\mathcal O(2^{\max d}\mathrm{poly}(n))$,其中 $d$ 是儿子个数。
考虑菊花图怎么做,因为所有儿子都是等价的,设 $g_{i,j}$ 表示当前值域填满了 $[0,i]$,用了 $j$ 个儿子的方案数,可以简单算出。
核心性质是点 $i$ 上标的数不会超过 $d_i$。对于一个点,如果其儿子个数比较少,可以用 $2^{d_i}$ 的状压。如果其儿子的度数的最大值比较小,则可以用 $2^{\max_v d_v}$ 的状压。考虑把这两个结合起来:设阈值 $B$,对于儿子数 $<B$ 的非叶子儿子,先进行 $2^B$ 的状压算出来方案数。然后把这个作为初值,因为儿子数 $>B$ 的儿子个数不会超过 $\frac n B$,所以接下来的答案不会超过 $B+\frac n B$,可以状压这个东西。最后再根据已经计算好的 $g$ 考虑叶子的贡献即可。取 $B=\sqrt n$ 则复杂度为 $\mathcal O(2^{2B}\mathrm{poly(n)})$。
实际上可以发现取一个 $B$ 之后,点 $i$ 的答案上界是 $B$ 加度数大于 $B$ 的儿子个数,这个对于每个点可以找一个最优的 $B$,经过分析可以发现复杂度是 $\mathcal O(2^{\sqrt{2n}}\mathrm{poly(n)})$,就过了。
T4
太难了。
Day 8
T1
先枚举 $a,b$ 存在桶里,然后枚举 $c,d$。
T2
从后向前填,填相对顺序。设 $f_{i,j}$ 表示填了 $[i,n]$ 的后缀,当前最小的 $s$ 是 $1$ 的位置填的相对大小是 $j$。转移就是找一个位置插进去,发现可以前缀和优化到 $\mathcal O(n^2)$。
T3
首先求出来 $b$ 表示距离,$l$ 表示所在环长。然后就是要找到最小的 $x$ 满足存在 $y$ 使得 $b+yl\in[Lx,Rx]$,可以先二分 $x$ 然后万欧做 floor_sum,总复杂度 $\mathcal O(n\log^2 n)$。
T4
首先考虑暴力 DP:设 $f_i$ 表示填满 $[1,i]$ 前缀的方案数。转移就是枚举当前 $[1,i]$ 作为印章用了几次,每次需要找到下一次的合法位置。
发现合法位置的限制是 $LCP(1,i)\geq k$,所以先跑一遍 Z 函数,然后就变成序列上找到 $i$ 后面 $\geq j$ 的第一个位置。可以线段树或者 ST 表维护做到单次查询 $\mathcal O(\log n)$。
具体就是初始 $p=i+1$,然后找到 $p$ 后面第一个 $LCP(1,j)\geq i$ 的位置 $q$,然后更新 $q+i-1$ 之后的所有部分,这里可以用前缀和优化一下,然后 $p=q+i$。然后因为 $p$ 每次都至少会增加 $i$,所以只会暴力跳 $\mathcal O(n\log n)$ 次,这样总复杂度是 $\mathcal O(n\log^2 n)$,还不够。
注意到查询满足 $\geq j$ 的限制是严格递增的,所以考虑并查集维护,每次把不合法的位置和 $i+1$ 合并起来,查询就是直接查询祖先结点了。这样复杂度就是 $\mathcal O(n\log n\alpha(n))$。
Day 9
傻逼。
T1
首先这玩意是下凸的。所以先判断一下 $0$ 合不合法,如果合法了就赢了,否则后面一定是存在一个点,使得在这个点之前不合法,之后合法,二分之后 nth_element 即可,总复杂度 $\mathcal O(n\log V)$。
T2
不知道为啥,每次贪心的取最大的 $n!$ 的因子即可,预处理出来之后跑二分。
T3
把 $0$ 的权值看成 $1$,$1$ 的权值看成 $-1$,则答案就是序列中 $1$ 的个数加上最大前缀权值和。reverse 之后选前缀可以看成先选一段前缀然后选 $k$ 个子串,可以线段树做反悔贪心。
T4
设 $f_{i,j}$ 表示 $i$ 子树内用了 $j$ 条例链来覆盖的最小权值,特别的,$f_{i,0}$ 表示子树内所有点走到 $i$ 的权值,这样转移是 $\min,+$ 卷积,并且这玩意显然是凸的,拿 set 什么的维护一下差分数组,可以 $\mathcal O(n^2\log n)$ 或者多一个 $\log$。
考虑如何优化,进行树上启发式合并。首先用可持久化线段树合并求出来每个子树的 $f$。然后对整个树做 dfs。
dfs 的时候用一棵值域线段树来维护子树外的 dp 数组的差分值,这样查询的时候就在两棵线段树上同时进行二分。
向下递归的时候,先把所有轻子树的差分数组合并到线段树上,然后向重子树递归,递归的时候加入重子树新的代价。然后往轻子树递归的时候先把贡献删了,再向下递归。这样总复杂度 $\mathcal O(n\log^2 n)$。
Day 10
T1
考虑怎么样会被算重:显然是两个长度和相同的,并且 $s_i=s_j$ 的时候,$S[1,i]+S[j+1,n]=S[1,i-1]+S[j,n]$ 才是一样的,所以只需要统计 $s_i=s_j$ 的个数即可。
T2
设 $f_{i,j,k}$ 表示走了 $i$ 步,从 $j$ 走到 $k$ 的方案数,转移:
\[\begin{aligned} f_{i,l,r}\overset +\leftarrow f_{i-1,l,k}t_{k,r}\\ f_{i,l,r}\overset -\leftarrow f_{i-1,l,k}t_{k,r}t_{r,k}\\ \end{aligned}\]其中 $t$ 是邻接数组。考虑矩阵套矩阵,同时记录相邻两次的状态即可,复杂度比较爆,需要一点手法,比如矩阵乘法的时候拿 ull 存数据,然后乘法 $18$ 次取模一次。
T3
还挺牛。
字典序限制从后向前做,考虑维护一个扩展域并查集。因为限制是需要恰好分成两个大小为 $n$ 的集合,所以需要判断 merge 了之后还能不能拼出来。考虑实时维护一个背包 $f_i$ 表示第一个背包的大小为 $i$ 的方案数。新加入限制的时候就先删去原先的贡献,然后加入新的贡献。如果 $f_n$ 仍然不为 $0$ 就能直接合并。
但是如果 $f_n=0$ 了那就不能合并,但是 $m$ 非常的大,$\mathcal O(mn)$ 不能接受。但是注意到不能合并那最终方案里一定是需要两者反着合并,所以可以反着将他们合并起来,这样一共只会合并 $n$ 次,时间复杂度均摊 $\mathcal O(n^2+m)$。
T4
抽象困难题。
Day 11
T1
考虑对于一个序列做上面的排序,经过第一轮之后序列的第一个会变成最大值,并且前缀最大值会向前移位一个。然后后面的轮的交换次数就是每个点前面本质不同的比他大的数的数量,这样就可以做到 $\mathcal O(n^2\log n)$。
优化比较 trival,考虑从前向后做,实时维护经过第一轮之后的序列,容易发现就是比较 $a_i$ 和当前的最大值,如果 $a_i$ 大于当前最大值就进行交换。然后本质不同前缀大于他的个数可以树状数组麻烦维护,时间复杂度 $\mathcal O(n\log n)$。
T2
考虑钦定一个点作为最大值,然后向下做,要求向外走的时候权值必须非增。但是钦定会算重,观察到最大值一定是一个联通块,所以进行点减边容斥,可以带 $-1$ 的系数钦定边作为最大值。
设 $f_{i,j,0/1}$ 表示 $i$ 点上填了 $j$,字数内是否钦定了根,转移:
\[\begin{aligned} g_{j,0}&\overset +\leftarrow \sum_{k\leq j}f_{v,k,0}f_{i,j,0}\\ g_{j,1}&\overset +\leftarrow \sum_{k\leq j}f_{v,k,0}f_{i,j,1}\\ g_{j,1}&\overset +\leftarrow \sum_{k\geq j}f_{v,k,1}f_{i,j,0}\\ g_{j,1}&\overset -\leftarrow f_{v,j,0}f_{i,j,0} \end{aligned}\]可以前缀和优化到 $\mathcal O(nm)$。然后可以进行一个非常麻烦的换根。
T3
感觉是唐,$f_{i,j,k,0/1,0/1}$ 表示当前两个路径端点在 $i,j$,填了 $[1,k]$ 的数,两边是开还是闭区间,转移均摊 $\mathcal O(n)$。
T4
好像挺简单的。。
首先考虑枚举答案 $k$,$<k$ 的看成 $-1$,$>k$ 的看成 $+1$,$k$ 看成 $0$。设 $f_{i,x,y,0/1/2}$ 表示当前在节点 $i$,非确定值的 $-1$ 的个数是 $x$,非确定值的 $1$ 的个数是 $y$,伪代码跑出来的结果是 $0/1/2$ 的方案数。
首先因为 $q$ 非常少,那把 $q$ 全设成 $0$ 可以求出下界,全设成 $m-1$ 可以求出上界。然后用原序列中出现过的数把值域划分,显然只有 $\mathcal O(q)$ 个段,先对这下答案跑上面的 DP,单次 DP 是可以用树形背包分析出打表发现复杂度是 $\mathcal O(q^4)$ 的。
然后要求 $\sum_{i=L}^R i^x(m-1-i)^y$,这个东西可以用拉格朗日插值在 $\mathcal O(q)$ 或者 $\mathcal O(q^2)$ 时间内求出。一共要做 $q$ 次 DP,插值 $q$ 次,总复杂度 $\mathcal O(q^5)$。
Day 12
T1
题唐。
T2
我唐。
枚举答案,判断可以想办法 $\mathcal O(m)$。
T3
definieren 神。
注意到一个数操作到 $>10^5$ 之后,想要抬高他的高度就需要操作一整段后缀一次。设 $g_{i,j}$ 表示 $a_i$ 先除了 $2^j$,然后增加到 $10^5$ 以上,并让序列在 $i$ 后面的部分也递增的最小代价,转移 $\mathcal O(n\log^2 n)$。
这样前面的 $\times 2$ 操作次数就是 $\mathcal O(\log n)$ 级别的,设 $f_{i,j,k}$ 表示 $a_i$ 先除了 $2^j$,再乘了 $2^k$,使得 $[1,i]$ 递增的最小代价,转移 $\mathcal O(\log(\log n))$。
T4
是凸的。平衡树维护转折点还有啥的就行了。
Day 13
我是傻逼。
T1
钦定一个点当根,后面每个节点填数方案数是确定的。
T2
矩阵长宽大于 $k$ 的时候可以进行一个缩,这样缩成 $k\times k$ 矩阵。然后随便判一下就行了。
T3
好唐。。。。。。。。。。
暴力 DP 是设 $f_{i,0/1,0/1}$ 表示当前在时刻 $i$,在左侧还是右侧,另一侧同位置的人之前有没有见过,转移 $\mathcal O(1)$。
不难注意到可以值域反转,因为时刻越小越好。然后就做完了。
T4
我是素质小子。
首先考虑二分后 $01$ 染色,从前往后扫,维护一个栈。如果栈顶有三个 $0$ 就直接消成一个 $0$。如果栈顶是 $1$,下面的一个试 $0$ 也能直接消成虚空(容易证明一定最优),然后如果某时刻栈顶出现了两个 $1$ 就赢了。线段树维护这个东西是两个 $\log$ 的。
一个挺离谱的东西是,在染好色的序列两端补 $1$,然后设第一个位置的下标是 $0$。如果存在 $i<j,i\equiv 0\pmod 2,j\equiv 1\pmod 2$,并且 $a_i=a_{i+1}=a_j=a_{j+1}=1$,则合法,否则不合法。
充分性是比较简单的(?),$i,j$ 之间可以缩成只剩一个 $0$,然后再操作 $i+1,j$,这样 $i,j$ 就靠在一起,形成了三个连续的 $1$。再考虑两端,剩下的 $0$ 也能缩成一个,所以最后就只剩一个 $1$ 了。
必要性的话就是你感觉他很必要。我不会证。
这样弄一下猫树什么的就能做到 $\mathcal O(n\log n+q)$。
Day 14
/kuk/kuk
可惜没打,感觉都挺简单(?)
T1
等价于 $AB$ 是完全平方数,枚举 $A$,要补一个最小的 $B_0$,则个数就是 $\lfloor\sqrt\frac m {B_0}\rfloor$。
如何计算应该补什么:线性筛一遍求出 $g_i$ 表示对于所有质因子,如果次数是奇数贡献就是 $p_i^{c_i+1}$,否则是 $p_i^{c_i}$,贡献乘积。
T2
这题是黑题啊我靠,以前好像觉得极其困难的来着。
对于每种颜色算贡献。容斥,算没有贡献的路径数。那就是要算把他的边全都断掉之后,每个连通块的 $\frac{s(s-1)}{2}$ 之和。
考虑直接 dfs,拿一个桶记录子树中所有颜色等于 $i$ 的边的子树 $siz$ 之和,查询就能直接查了。往下递归的时候注意要先删贡献(不让子树外对子树内产生影响),回溯的时候再加回来。复杂度 $\mathcal O(n)$。
T3
我好厉害!
先二分答案转成 chk。可以发现 $S$ 左边的每时每刻向右走,$S$ 右边每时每刻向左走不劣,并且 $S$ 停在原题不优(可以通过决策包容性说明)。
进一步观察,$S$ 和某个点重合了之后,立刻分开也不优,保持挨在一起到某个人似掉是不劣的。因为左右内部相对顺序不改变,所以可以看成向左合并是花费 $\frac{x_i-x_{i-1}}{2v}$ 的代价获得 $T$ 的收益,向右同理,要求每时每刻 $T\geq 0$。可以看成是有一个网格图,点 $(i,j)$ 的权值是 $a_i+b_j$,只能走权值 $\geq 0$ 的点。和去年 NOIP T3 双序列扩展 一模一样了。
T4
纯唐,枚举每个点对,ban 掉的是一段 dfn 矩形,拿线段树暴力做扫描线就行了。
Day 15
T1
枚举一个边长,则每种颜色有贡献,要求的是矩形左上角在某个矩形区域内,做扫描线即可。
T2
二分答案。把 $\geq x$ 的数标成 $1$,$<x$ 的数标成 $0$。可以发现删 $1$ 一定不优(不如删它后面第一个 $0$),一定是把 $0$ 全删了之后剩下了全 $1$,然后任意删。
然后考虑删 $0$ 的过程中如何收益最大化。对于一个 $1$ 的连续段,如果长度是偶数,则贡献确定。如果长度是奇数,先和偶数一样算一下确定的答案。不确定的部分就是当他的开头在奇数位置的时候他可以多 $1$ 的贡献。上界显然就是他 后面 $0$ 的个数 加上 前面 $0$ 的个数除 $2$ 上取整或者下取整 。复杂度 $\mathcal O(n\log n)$。
T3
没有限制就是建一个虚点,向奇度数点连边跑欧拉回路。
有限制之后,考虑找出每个连通块,把两条边缩在一起就能保证是偶数了。建个 dfs 树随便做做就行。
T4
K=2
就是求两条边都在这个区间内的方案数。直接二维数点就行。
K=3
求走两条边仍然在这个区间内。第一种情况是走两条边回到自己,这个答案就是区间度数和。
第二种情况是走到一个中转点。考虑进行根号分治,如果中转点的度数 $\geq B$,则进行特殊处理:枚举中转点和询问,先计算前缀和,这样每个询问可以 $\mathcal O(1)$ 计算出区间内有多少个中转点的邻点。
对于中转点度数 $<B$ 的情况,可以套用上面二维数点的方法。但是用 BIT 会多半只 $\log$,维护一个支持 $\mathcal O(1)$ 单点加,$\mathcal O(\sqrt n)$ 查询的分块就行了。复杂度是 $\mathcal O((n+q)\sqrt n)$。
Day 16
不难。
T1
乱数位 DP 就行了。
T2
预处理 $f_i$ 表示 $[1,i]$,然后在 $i$ 放置了一个支撑架的最小代价,转移单调队列优化,遇到一个 $s_i=1$ 就把单调队列清空就行。用相同的方法处理出 $g_i$ 表示后缀的答案。修改之后随便拼起来就行,复杂度 $\mathcal O(n+kq)$。
T3
把排列拆成若干个置换环。把苹果排序,一个环一定是分到连续的一段苹果。然后一段苹果分给一个环的最小代价就是 $1,3,5\dots n,n-1,n-3\dots 2$ 这样放。可以预处理出来代价。
然后状压 DP,状压当前长度为 $k$ 的置换环还剩几个,转移就是新加一个置换环。复杂度大概是 $\mathcal O(2^{\sqrt n})$ 级别,实际稍微大一点但是完全能跑。
T4
懒得喷,谁家跑路要问能到的安全度之和啊。不都是问最大值。
考虑淀粉,预处理 $f_i$ 表示从当前分治重心走到 $i$ 的初始最大危险度。还有找出能走到分治重心的点的 $g_i$ 表示其走到分治重心时的危险度。这样处理贡献就是归并一下,树状数组做一个二维数点即可。复杂度 $\mathcal O(n\log^2 n)$。
Day 17
唐完了。
T1
答案上界是 $\lfloor\frac n 2\rfloor(n-\lfloor\frac n 2\rfloor)(2^{t+1}-1)$,其中 $t$ 是满足 $2^t\leq m$ 的最大整数。判掉 $m=1$ 后可以发现上界都是可以取到的。放 $\lfloor\frac n 2\rfloor$ 个 $2^t$,$n-\lfloor\frac n 2\rfloor$ 个 $2^t-1$,就行了。
T2
哎哎。
多尝试几次发现,按照 $b_i$ 从小到大排序,选择干掉 $b_i$ 的话一定是一段前缀里面挖去几个,并且挖去的一定是当成 $a_i$ 杀掉。
这样就可以直接 DP 了。先枚举一共杀掉 $x$ 个 $b$,设 $f_{i,j}$ 表示当前前缀 $i$ 杀掉了 $j$ 个的最小代价,转移平凡。
统计答案的时候还需要预处理 $g_i$ 表示从 $[i+1,n]$ 中选出 $m-i$ 个最小的 $a$ 的和,答案就是 $f_{i,x}+\frac{g_i}{x+1}$。
T3
哎哎。
在串相邻的字符之间填上 $>,=,<$ 三种符号,限制就是要求在 $[x,y)$ 区间内第一个不为 $=$ 的符号需要是 $>$ 还是 $<$。
考虑如果在 $i,i+1$ 之间是大于号,则找到一个 $x\leq i<y$ 并且要求是小于号的限制,那就要求上一个不为等号的符号在 $[x,i-1]$ 之间。感觉这个思想非常典啊,扔给上一个处理 QwQ。
然后可以 DP 了,$f_{i,j,0/1}$ 表示当前在 $i$ 填了 $j$,下一个字符需要填比 $j$ 大的还是小的。每次向后转移一段区间。前缀和可以把复杂度优化到 $\mathcal O(n\Sigma+n\log n)$。
T4
见过三次了哥们。
Day 18
T1
考虑差分,一次操作 $[l,r]$ 会影响 $b_l$ 和 $b_{r+1}$。把操作看成连接 $(l,r+1)$ 的边,就是要找若干个树,使得树的权值和是零并且树最多。
状压 DP,每次扩一个连通块太慢,只扩一个点,转为统计前缀和为 $0$ 的次数也是对的。
T2
先判掉明显不合法的:$b_i>b_{i+1},b_1=n+1,b_i<i$ 等。
考虑颜色数的上界是 $\min\{b_i-i+1\}$。直接取这个上界。
设 $pre_i$ 表示上一个和 $i$ 颜色一样的点。一个区间 $[i,b_i]$ 的限制是 $pre_{b_i}=i-1$,且不存在 $j>b_i\wedge pre_j<i$。
从前向后扫一遍,如果当前点的 $pre$ 还未确定,如果用过的颜色数还小于上界就新开一个颜色,否则因为要满足第二个限制,先取靠前的颜色是更优的,所以就取 是当前最后一次出现的颜色 的出现位置的最小值作为 $pre$。
T3
设 $f_{l,r}$ 表示区间 $[l,r]$ 消空了,并且 $l-1,r+1$ 都没有和任何一个数发生合并的最大收益。
转移是枚举区间内消除的最后一个数,其可能是若干个数拼起来。枚举这若干个数中最右边的一个,所以设 $g_{l,r}$ 表示区间 $l,r$ 清空,清空的最后一个数是 $r$ 和前面的若干个数并起来的结果的最大收益。
求 $g$ 就设 $h_{l,r,x}$ 表示区间 $[l,r]$ 内剩了一个大小为 $x$ 的,由 $r$ 和其他数字合并起来的数字,此时的最大收益,转移就是两段 $h$ 拼起来,复杂度 $\mathcal O(n^3k^2)$,因为是区间 DP 所以有一个 $\frac 1 6$ 的常数,$k$ 这一维做背包所以有一个 $\frac 1 2$ 的常数。
T4
不会。
Day 19
T1
按照右端点排序,set 维护可用的人的第一个可用时刻,每次贪心找到小于等于 $l$ 的最大的点,把他删掉,并把 $r$ 加入集合。
T2
预处理 $f_i$ 表示 $i$ 子树内 dfs 序数量。
向下走的时候,处理出 $g_{i,j}$ 表示选了 $u$ 的 $i$ 个子树,$siz$ 和为 $j$,每次除去一个再卷上去即可。复杂度 $\mathcal O(n^3)$。
T3
从小到大排序。可以证明一个点的贡献可以是 $i<j<n,a_j-a_i$ 的任意值。bitset 优化一下背包就行了。
T4
感觉挺简单的。
先找到第一个区间里的最大值 $x$,然后查询第二个区间里 $<x$ 的最大值 $y$。如果 $\lfloor\frac{x}{2}\rfloor\leq y$ 就赢了,答案就是 $x+y$。
否则一定会选 $y$,在第一个区间里找到 $\lfloor\frac{x}{2}\rfloor\leq y$ 的最大 $x$,再判合法性。
容易发现这样找两轮,数字大小就会除 $2$。拿一个主席树支持上面的操作即可。复杂度 $\mathca O(n\log V\log n)$。
Day 20
太他妈傻逼了,能 AK 的场打成这个样。。。
T1
看成是选一个 $k$,再选 $k$ 个数,其乘积 $>n$ 并且 $ka+\sum_{j=1}^k(a_j-1)b$ 最小。调整法可以证明 $a$ 只有相邻的两种取值,枚举 $k$ 即可。
T2
想让 $\text{mex}=0$ 就需要存在相邻的两个 $0$ 之间的距离大于区间长度。基于这个,维护所有相邻相同数的差值,放进一个线段树里,每次线段树上二分即可。
T3
很有水平,会做,但是赛时不会半在线卷积,今天糊出来了一个做法/oh/oh/oh。
设 $f_{S,i}$ 表示,当前 $S$ 集合内的人还存活,还有 $i$ 道对当前没有影响的题目没有用。没有影响指的是加入了不会导致任何一个人淘汰。转移是转移到 $f_{S,i-1}$,或者枚举一个使集合变化的题目和集合求交。
转置一下,即把上面这个过程反过来做。可以发现第二维是没有用的,预处理出 $in_S$ 表示对集合 $S$,没有影响的题目,这是一个高维前缀和。每次形如扩张一个 $S\rightarrow T$,乘一个 $\binom{n-in_T+(in_T-in_S-1)}{in_T-in_S-1}$,表示把一些无用题目变成了有用题目,插入到题目序列最后面的位置。而且这个组合数只和 $S,T$ 分别有关。
但是还要对所有点求答案,所以再对上面的过程转置一下(?),还是从前向后做就行了。这样可以做到 $\mathcal O(n2^m)$。
因为之和 $S,T$ 有关,所以转移形如,枚举 $k\in[1,n]$,$T\leftarrow S\cup A_k$。这是一个 and 半在线卷积,赛时就是卡在这一步了。
从大到小枚举 $S$ 的 popcount 大小,每次只考虑这些 $S$,对他们和 $A_k$ 进行一个 and 卷积,只保留对 popcount 小于 $S$ 的 dp 值的贡献即可。一共 $m$ 次半在线卷积,复杂度 $\mathcal O(m^22^m+n)$。
T4
主主主,文爪 7 升桂 3。
考虑归并排序,现在就是要把两个序列合并。再进行一步分治,吧奇偶位分别归并一下。观察此时的序列,可以发现只有 $2k,2k+1$ 的一个位置可能需要调整,所以开一层比较所有 $2k,2k+1$ 的比较器就行了。操作次数是 $\mathcal O(log^2n)$ 的,有一个 $\frac 1 2$ 的常数,一共 $28$ 次。