My Blogs
[ARC177F] Two Airlines
有点魔怔的题。
一个基本的观察是如果当前某个人 $A$ 拿着盒子走到了位置 $i$,那位置小于 $i$ 的人一定永远没用了。如果之后要用到前面的人 $B$,就应当让 $B$ 拿着盒子走到 $i$ 而不是让 $A$,这样 $A$ 待在原来的位置,代价一定不会更劣。
再手玩一下,可以发现每次的过程都是:某个人 $A$ 拿起盒子,走到某个地方。然后后面来了一个和 $A$ 颜色不一样的人(或者是本身就在这个地方的人),走到了 $A$ 现在的位置,然后带着箱子走了,此时 $A$ 也已经没有用了。
进一步的,“后面来人”的这个过程,对于每种颜色内部,一定是先用坐标尽量小的人来。这个结论不难用调整法证明。
而最优解一定能用上述过程刻画出来。所以可以设 $f_{i,j,k,0/1}$ 表示当前盒子在 $i$,被 $0/1$ 颜色的人拿着,$i$ 后面的 $j$ 个颜色为 $0$ 的人已经用过了(此时在 $<i$ 的位置),$k$ 个颜色为 $1$ 的人已经用过了。转移 $\mathcal O(1)$,状态数和复杂度都是 $\mathcal O(n^3)$ 的。
接下来的一个想法观察性质,能不能简化一维状态什么的,但是好像不太好做。除此之外比较自然地,可以感受到 $j,k$ 都不会太大,设成 $20$ 左右,交上去就直接过了。下面证明 $j,k$ 都只需要取到 $\log n$。
直观感受一下,“后面来人”的原因一定是,$i$ 后面有一段比较长的和当前拿着箱子的颜色不同的路。
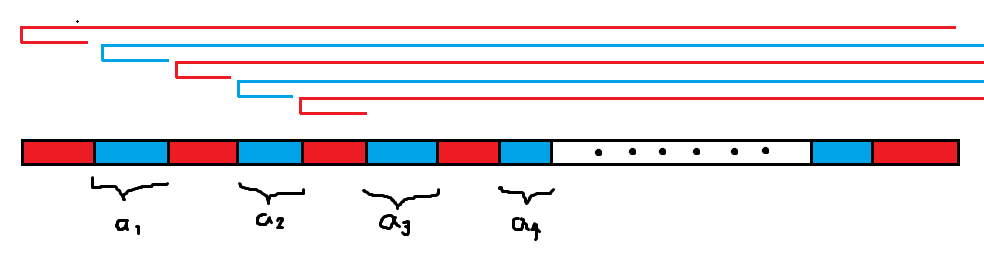
红色和蓝色的块分别表示序列上红色和蓝色的连续位置。红色段里面不一定全部都是红色,蓝色段里也不一定全是蓝色。红色和蓝色的线条表示人走过的路程。$a_i$ 表示这个蓝色段里面有多少个蓝色格子。
称除去搬运盒子过程中造成的代价为“额外代价”。因为第二条红色线条走到他的目标位置(第二个红块)额外花费了 $\sum_{j\geq 2}a_j$ 的代价,所以 $a_1>\sum_{j\geq 2}a_j$,否则可以让第一个人直接走到第二个红色段:
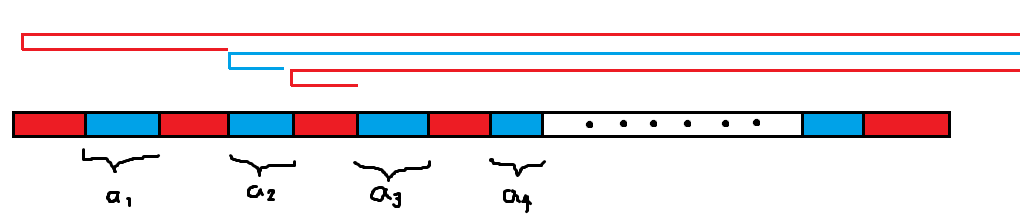
这样一定不劣。后面的同理,$a_i>\sum_{j>i}a_j$,所以最多 $\log$ 轮之后 $a_i$ 就要超出值域了。所以 $j,k$ 的维度都只需要开到 $20$。预处理一下还是能做到 $\mathcal O(1)$ 转移。总复杂度 $\mathcal O(n\log^2 n)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int n,m,f[60010][21][21][2],nex[2][60010][21],t[60010][2],a[60010][2];
char s[60010];
vi ve[2];
inline void mian()
{
read(n,m),read(s);int x,ans=INF;char ch;
while(m--)read(x),read(ch),t[x][ch=='A']++,ve[ch=='A'].eb(x);
for(int i=1;i<=n;++i)a[i][0]=a[i-1][0],a[i][1]=a[i-1][1],++a[i][s[i]=='A'];
sort(ve[0].begin(),ve[0].end()),sort(ve[1].begin(),ve[1].end());
for(int k=0;k<2;++k)for(int i=0;i<=n;++i)
{
int p=lower_bound(ve[k].begin(),ve[k].end(),i)-ve[k].begin();
for(int j=1;j<=20;++j)
if(p+j-1<(int)ve[k].size())nex[k][i][j]=ve[k][p+j-1];
else nex[k][i][j]=-1;
}
memset(f,127,sizeof(f));
if(nex[0][0][1]!=-1)f[0][1][0][0]=a[nex[0][0][1]][1];
if(nex[1][0][1]!=-1)f[0][0][1][1]=a[nex[1][0][1]][0];
for(int i=0;i<n;++i)
{
for(int j=0;j<=20;++j)for(int k=0;k<=20;++k)
{
if(j<20&&nex[0][i][j+1]!=-1)Mmin(f[i][j+1][k][0],f[i][j][k][1]+a[nex[0][i][j+1]][1]-a[i][1]);
if(k<20&&nex[1][i][k+1]!=-1)Mmin(f[i][j][k+1][1],f[i][j][k][0]+a[nex[1][i][k+1]][0]-a[i][0]);
}
for(int j=0;j<=20;++j)for(int k=0;k<=20;++k)for(int l=0;l<2;++l)
Mmin(f[i+1][max(0ll,j-t[i][0])][max(0ll,k-t[i][1])][l],f[i][j][k][l]+(l!=(s[i+1]=='A')));
}
for(int i=0;i<=20;++i)for(int j=0;j<=20;++j)for(int k=0;k<2;++k)Mmin(ans,f[n][i][j][k]);
write(ans);
}