My Blogs
CF1534G A New Beginning
不太懂为啥是黑。需要先会基本的 slope trick。
首先切比雪夫距离可以转成曼哈顿距离但是没啥必要。因为只能向右上走,所以考虑把每个关键点归到它属于的斜率为 $-1$ 的直线上,即按照 $x_i+y_i$ 排序分类。
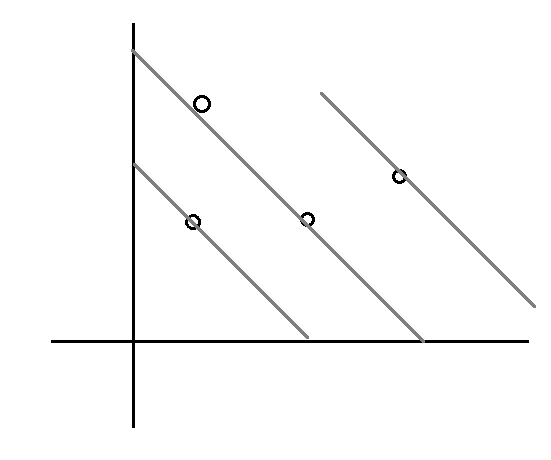
容易发现一定是走到了某条灰线上之后再收取该灰线上的所有点。所以设 $f_{i,j}$ 表示走到了第 $i$ 条线,当前横坐标为 $j$ 的最小代价。
然后感觉一下,固定了 $i$ 这个东西关于 $j$ 很像是凸的。实际上可以证明这个东西是凸的。考虑归纳,首先从上一条线到这一条线的转移形态:
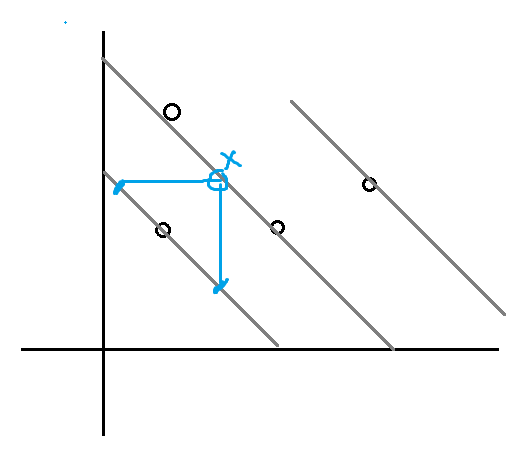
点 $x$ 能从上一条线蓝色的部分转移而来,那对应到函数图像上:
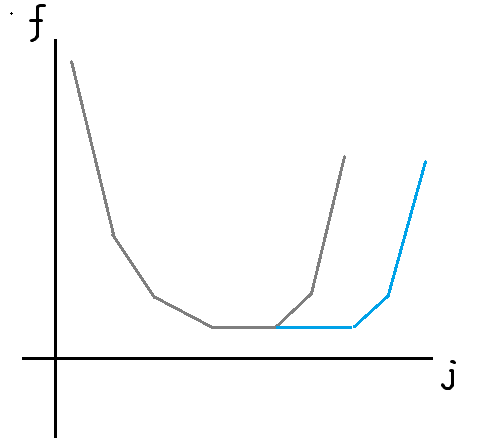
可以发现是把斜率大于 $0$ 的部分像右移动了一段长度。然后对于这条线上的所有关键点,其对于 $f$ 的贡献是一个绝对值函数($\lvert j-x_i\rvert$)。然后凸函数加凸函数还是凸的,所以归纳成立。
维护这个东西的话,就是开一个对顶堆,维护最低段左侧和右侧的所有拐点。加入一个绝对值函数的时候,根据其和最低的一段的关系分类讨论一下即可(这时可能会出现左侧堆的点跑到右侧堆里去或者相反)。
最后计算答案的时候,由题意得 $f(0)=\sum x_i$,然后可以根据这个和左侧堆内的信息来推出最低点的纵坐标(实际上就是减去左侧堆的所有点的横坐标)。总复杂度 $\mathcal O(n\log n)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int n,len,tg,numa[800010];
pii a[800010];
vector<int> ve[800010];
priority_queue<int> q1;
priority_queue<int,vector<int>,greater<int>> q2;
inline void mian()
{
read(n),q1.e(0),q2.e(0);int s=0;
for(int i=1;i<=n;++i)read(a[i].fi,a[i].se),numa[++len]=a[i].se+a[i].fi,s+=a[i].fi;
sort(numa+1,numa+1+len),len=unique(numa+1,numa+1+len)-numa-1;
for(int i=1;i<=n;++i)ve[lower_bound(numa+1,numa+1+len,a[i].se+a[i].fi)-numa].eb(a[i].fi);
for(int i=1;i<=len;++i)
{
tg+=numa[i]-numa[i-1];
for(auto p:ve[i])
{
if(q1.top()<=p&&p<=tg+q2.top())q1.e(p),q2.e(p-tg);
else if(p<q1.top())q2.e(q1.top()-tg),q1.pop(),q1.e(p),q1.e(p);
else q1.e(q2.top()+tg),q2.pop(),q2.e(p-tg),q2.e(p-tg);
}
}
while(q1.size())s-=q1.top(),q1.pop();
write(s);
}