My Blogs
P10541 [THUPC2024] 研发计划
首先看上去就比较像流,直接考虑怎么建模。
如果没有 $h$ 就是裸的最大权闭合子图:$S$ 向每个技术连边,每个收益向 $T$ 连边,然后技术指向收益的边连 inf,做最小割(割掉的表示支付的代价),答案就是收益之和减去最小割。
现在有了 $h$,要做的大概形如:如果一堆技术全都割掉了和 $S$ 的边,那某个技术代价可以更小。首先要割掉的是 $h$ 或者 $f$,所以两者应当是串联的。然后稍微尝试一下就能发现 $h$ 应该连在前面:
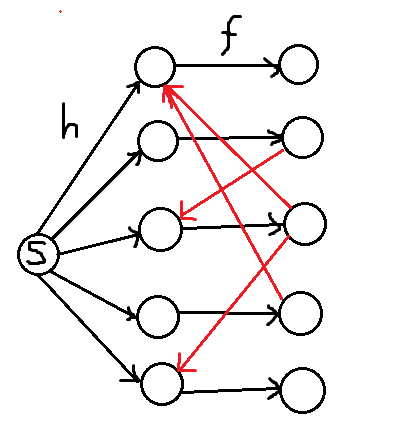
上图表示 $3,4$ 是 $1$ 的前置,然后 $3$ 是 $5$ 的前置,$2$ 是 $3$ 的前置。可以发现这样建模只有所有前置都被割掉才会割 $h$,否则割的是 $f$,然后跑 dinic 即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
int n,m,X,Y,S,T;
int cnt=1,head[410],to[100010],nex[100010],v[100010],now[410],d[410];
inline void Add(int x,int y,int z){to[++cnt]=y,v[cnt]=z,nex[cnt]=head[x],head[x]=cnt;}
inline void add(int x,int y,int z){Add(x,y,z),Add(y,x,0);}
queue<int> q;
inline bool bfs()
{
while(!q.empty())q.pop();
q.e(S),memset(d,0,sizeof(d)),d[S]=1,now[S]=head[S];
while(!q.empty())
{
int nw=q.front();q.pop();
for(int i=head[nw];i;i=nex[i])
{
if(!d[to[i]]&&v[i])
{
d[to[i]]=d[nw]+1,now[to[i]]=head[to[i]],q.e(to[i]);
if(to[i]==T)return 1;
}
}
}
return 0;
}
int dinic(int x,int flow)
{
if(x==T)return flow;
int rest=flow,t;
for(int i=head[x];i&&rest;i=nex[i])
{
now[x]=i;
if(!v[i]||d[to[i]]!=d[x]+1)continue;
t=dinic(to[i],min(rest,v[i]));
if(!t)d[to[i]]=0;
v[i]-=t,v[i^1]+=t,rest-=t;
}
return flow-rest;
}
inline void mian()
{
read(n,m,X,Y),S=3*n+m+1,T=S+1;int x,y,ans=0;
for(int i=1;i<=n;++i)read(x),add(S,i,INF),add(i+n,i+n*2,x);
for(int i=1;i<=n;++i)read(x),add(i,i+n,x);
for(int i=1;i<=m;++i)read(x),add(3*n+i,T,x),ans+=x;
while(X--)read(x,y),add(x+n*2,y+n*3,INF);
while(Y--)read(x,y),add(x+n*2,y+n,INF);
while(bfs())while((x=dinic(S,INF)))ans-=x;
write(ans);
}