My Blogs
[ARC176F] Colorful Star
感觉很考验想象力和计数基本功 QWQ。
首先考虑给定了局面之后如何进行判定。考虑把覆盖的过程倒着做:如果 $i$ 旁边有和它颜色相同的棋子,那它就可以变成任意的颜色,然后要求最终能不能 $n$ 种颜色都只剩一种。
然后这个还是不太本质。考虑如果有一个能变成任意颜色的,可以把它变成周围的另一个颜色,然后另一个颜色就能变成任意的颜色。
这样可以看成是空位的移动。问题变成了:在棋盘上有 $n$ 种颜色的棋子和若干个空位。当两个同色棋子相遇的时候可以把其中一个变成空位,可以把棋子移动到相邻的空位。问最后能不能每种棋子只剩一个且分别待在正确的链上。
进一步分析:考虑有多少个空格的时候,不论棋盘形态如何,都能消完。显然把初始相邻相同的消掉之后,接下来的相同颜色的消除操作(下称合并)一定是在中间位置发生的。
考虑如果只剩一个,不合法当且仅当把空位移到中心点之后中心点周围颜色全不相同。
如果只剩两个,不合法当且仅当把空位移到中心点和它周围的一个点之后,周围颜色有 $n-1$ 种,且第二圈全部都是剩下的一种颜色。
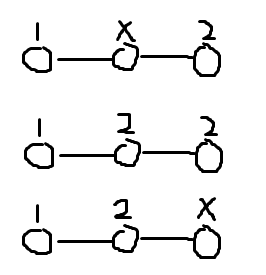
其中 $x$ 表示空位。
如果剩下了大于等于三个,则可以发现,能够通过若干个操作把周围两圈里的任意两个放到一起,判掉 $n\leq 2$ 的情况后,通过抽屉原理得一定能继续消,所以一定能消完。
接下来就是计数(下文中把图看成一棵以中心点为根的树):
-
初始没有空位,答案是 $n\times(n-1)^{nm}$。
-
初始有一个空位,并且之后周围的颜色全部不同,答案是 $n!\times nm\times(n-1)^{n(m-1)}$。其中 $n!$ 表示把空格移到中间之后周围的一圈数字的顺序,$nm$ 表示选择哪个位置和其父亲颜色相同。这样用去了 $n+1$ 个位置,剩下的位置随便填。
-
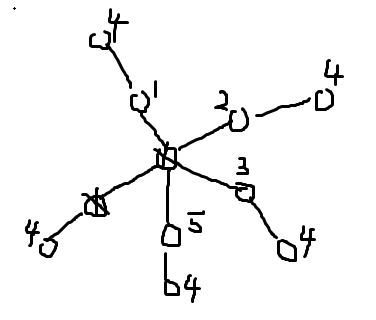
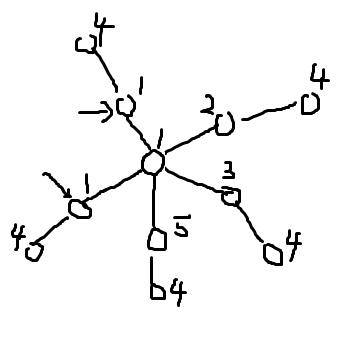
初始有两个空位,两个空位都是相邻相等的颜色消出来的。答案是 $n!\times \binom {nm} 2(n-1)^{n(m-2)}$。$n!$ 还是确定颜色的顺序,然后需要选两个位置和父亲相同,容易发现无论选哪两个位置都是合法的,譬如假如选了靠近根的两个点,那就代表这种情况:
其余的情况可以自行脑补。
由于需要确保中心点周围一圈都不同并且再外面一圈都是剩下的一种颜色,这样会用去 $n+(n-1)$ 个位置,然后选两个和父亲相同,剩下了 $nm-2n$ 个位置的方案数的唯一要求就是不能和父节点相同,$n-1$。
- 初始有一个空位,把这个空位移到中间之后再生出一个空位。首先需要确定空位产生的位置 $nm$,然后从 $n-1$ 个子树里面选两个临近根的点作为两个颜色相同,把空位移上来能消掉的。然后还要确定颜色顺序的 $n!$,最后剩下的位置仍然是 $nm-2n$,所以答案为 $n!\times nm\times\binom {n-1}2\times (n-1)^{n(m-2)}$。
最后用总和减去这四种不合法的就是答案。需要特判 $n=1,n=2$ 和 $m=1$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int n,m,fr;
inline void mian()
{
read(n,m),fr=1;
for(int i=1;i<=n;++i)Mmul(fr,i);
if(n==1)return write(1);
if(n==2)return write(Cadd(Cmul(n,m),2));
if(m==1)
{
int all=power(n,n+1);
int x=Cmul(n,power(n-1,n));
Madd(x,Cmul(n,Cdel(fr,1)));
return write(Cdel(all,x));
}
int all=power(n,n*m+1);
int x0=Cmul(n,power(n-1,n*m));
int x1=Cmul(n,m,fr,power(n-1,n*m-n));
int x2=Cmul(n,fr,power(n-1,n*m-2*n),m,m-1,inv2);
Madd(x2,Cmul(fr,n,n-1,inv2,m,m,power(n-1,n*m-2*n)));
Madd(x2,Cmul(fr,n,n-1,n-2,inv2,power(n-1,n*m-2*n),m));
write(Cdel(all,x0,x1,x2));
}