My Blogs
[ARC176E] Max Vector
$n=10$ 其实有点误导性。其实这个题不是指数级的算法,而且贪心也不是很合理,同时“要么…要么…”有点像最小割。
一次操作可以看成要求 $x_j\geq a_{i,j}$ 或者 $y_j\geq a_{i,j}$。考虑切糕的模型,建 $2n$ 条链,割哪条边就表示第 $i$ 个变量的取值。其中 $x_i$ 的链要正着建,$y_i$ 的链要反着建:
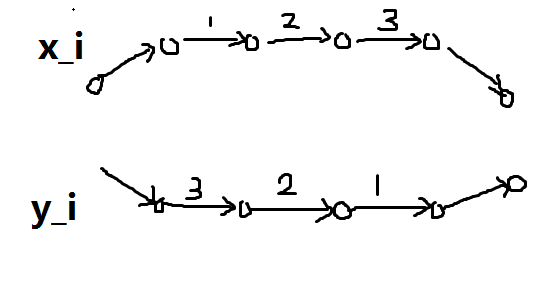
对于每次操作,建一个点 $i$,向 $2n$ 条链连边,其中向 $x$ 的是出边,假设权值是 $a_j$,则向第 $j$ 条链上的第 $j$ 个点连边,容量 inf。向 $y$ 的是入边,从第 $j$ 条链上的第 $v-a_j+2$ 个点连边向 $i$。
这样,就刻画出了“${\forall i,x_i\geq a_i}\lor{\forall i,y_i\geq a_i}$” 。直接跑最大流就是答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
const int N=300000,M=3000000,V=500;
int n,m,S,T,s,cnt=1,now[N+10],head[N+10],to[M+10],nex[M+10],v[M+10],d[N+10];
inline void Add(int x,int y,int z){to[++cnt]=y,v[cnt]=z,nex[cnt]=head[x],head[x]=cnt;}
inline void add(int x,int y,int z){Add(x,y,z),Add(y,x,0);}
queue<int> q;
inline bool bfs()
{
while(!q.empty())q.pop();
q.e(S),memset(d,0,sizeof(d)),d[S]=1,now[S]=head[S];
while(!q.empty())
{
int nw=q.front();q.pop();
for(int i=head[nw];i;i=nex[i])
{
if(!d[to[i]]&&v[i])
{
now[to[i]]=head[to[i]],d[to[i]]=d[nw]+1,q.e(to[i]);
if(to[i]==T)return 1;
}
}
}
return 0;
}
int dinic(int x,int flow)
{
if(x==T)return flow;
int rest=flow,t;
for(int i=now[x];i&&rest;i=nex[i])
{
now[x]=i;
if(!v[i]||d[to[i]]!=d[x]+1)continue;
t=dinic(to[i],min(rest,v[i])),rest-=t;
if(!t)d[to[i]]=0;
v[i]-=t,v[i^1]+=t;
}
return flow-rest;
}
#define id(i,j) ((i-1)*(V+1)+j)
inline void mian()
{
read(n,m),S=n*2*(V+1)+m+1,T=S+1;int x;
for(int i=1;i<=n;++i)
{
read(x),add(S,id(i,x),inf),add(id(i,V+1),T,inf);
for(int j=1;j<=V;++j)add(id(i,j),id(i,j+1),j),v[cnt]=inf;
}
for(int i=n+1;i<=n*2;++i)
{
read(x),add(S,id(i,1),inf),add(id(i,V+2-x),T,inf);
for(int j=1;j<=V;++j)add(id(i,j),id(i,j+1),V-j+1),v[cnt]=inf;
}
for(int i=1;i<=m;++i)for(int j=1;j<=n;++j)
read(x),add(i+n*2*(V+1),id(j,x),inf),add(id(j+n,V+2-x),i+n*2*(V+1),inf);
while(bfs())while((x=dinic(S,inf)))s+=x;
write(s);
}