My Blogs
有点恐怖。
首先 $R,C$ 很不平衡,考虑用一棵竖着的线段树维护较大的 $R$ 维,每个节点上需要存的是 $C\times C$ 的数组 $d$,$d_{i,j}$ 表示该节点的最上面一行第 $i$ 个到最下面一行第 $j$ 个的最短路。
因为已经处理好了左右儿子内部的最短路,所以只需要枚举 $mid$ 处经过了哪条边。这是一个 $(\min,+)$ 矩阵乘法,暴力做是 $\mathcal O(RC^3+mC^3\log R+q)$,直接爆了。
瓶颈在于合并的复杂度太高。经过观察发现其有决策单调性:
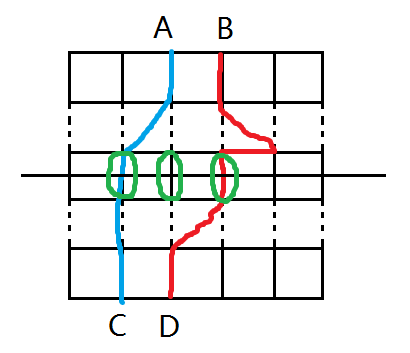
如果红色和蓝色分别是 $A\rightarrow C$ 的最短路和 $B\rightarrow D$ 的最短路,则 $A\rightarrow D$ 的最短路一定在三条绿色的线中。假设最短路穿过了红线或者蓝线,则一定会穿过两次。在这两次穿过的点之间,一定是选择原先的最短路最优。所以满足决策单调性,可以用类似区间 DP 的方式做到 $\mathcal O(C^2)$。
但是这样空间会炸:$10000\times 200\times 200$ 个 int 肯定开不下。考虑经典卡空间方式:底层 $\log$ 分块,线段树的底层不递归到 $L=R$,而是在 $R-L+1\geq 16$ 的时候就停下来暴力求出上面的点到下面的点的最短路,复杂度还是不变,但是空间除了一只 $\log$,大概只需要开到 $1500\times 200\times 200$。
暴力也有一些细节,不能最暴力的跑最短路 $\mathcal O(16C^2\log(16C))$ 复杂度会爆掉。枚举每个起点,进行朴素 DP,下设 $c_{x,y}$ 表示枚举的起点到 $x,y$ 的最短路:
\[\begin{aligned} c_{x,y}&=c_{x-1,y}\\ \mathrm{chkmax}&(c_{x,y},c_{x,y-1}+b_{x,y-1})\\ \mathrm{chkmax}&(c_{x,y},c_{x,y+1}+b_{x,y})\\ \end{aligned}\]两个 $\mathrm{chkmax}$ 操作只需要从左向右扫一遍,再从右向左扫一遍,这样一定不会错过最优解。
看起来比较吓人实际上是比较好写的。总时间复杂度是 $\mathcal O(RC^2+mC^2\log R+q)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
int cnt=1,n,m,q,a[5010][210],b[5010][210],p[210][210],c[201];
namespace Segment
{
#define ls(x) t[x].ls
#define rs(x) t[x].rs
#define cost t[ls(x)].d[i][k]+t[rs(x)].d[k][j]+b[mid][k]
struct{int ls,rs,d[201][201];}t[1510];
inline void update(int x,int L,int R)
{
int mid=L+((R-L)>>1);memset(t[x].d,127,sizeof(t[x].d));
for(int i=m;i>=1;--i)for(int j=1;j<=m;++j)
{
for(int k=p[i][j-1];k<=p[i+1][j];++k)
if(Mmin(t[x].d[i][j],cost))p[i][j]=k;
}
}
inline void calc(int x,int L,int R)
{
for(int i=1;i<=m;++i)
{
c[i]=0;
for(int j=i-1;j>=1;--j)c[j]=c[j+1]+a[L][j];
for(int j=i+1;j<=m;++j)c[j]=c[j-1]+a[L][j-1];
for(int j=2;j<=R-L+1;++j)
{
for(int k=1;k<=m;++k)c[k]+=b[L+j-2][k];
for(int k=2;k<=m;++k)Mmin(c[k],c[k-1]+a[L+j-1][k-1]);
for(int k=m-1;k>=1;--k)Mmin(c[k],c[k+1]+a[L+j-1][k]);
}
memcpy(t[x].d[i],c,sizeof(c));
}
}
void build(int p,int L,int R)
{
if(R-L+1<=16)return calc(p,L,R);
int mid=L+((R-L)>>1);
build(ls(p)=++cnt,L,mid),build(rs(p)=++cnt,mid+1,R),update(p,L,R);
}
void change(int p,int L,int R,int x)
{
if(!t[p].ls)return calc(p,L,R);
int mid=L+((R-L)>>1);
if(x<=mid)change(ls(p),L,mid,x);
else change(rs(p),mid+1,R,x);
update(p,L,R);
}
}
using namespace Segment;
inline void mian()
{
read(n,m);int opt,x,y,z;
for(int i=1;i<=m;++i)p[i][m+1]=m,p[i][0]=1,p[m+1][i]=m,p[0][i]=1;
for(int i=1;i<=n;++i)for(int j=1;j<m;++j)read(a[i][j]);
for(int i=1;i<n;++i)for(int j=1;j<=m;++j)read(b[i][j]);
build(1,1,n),read(q);
while(q--)
{
read(opt,x,y),++x,++y;
if(opt==1)read(z),a[x][y]=z,change(1,1,n,x);
else if(opt==2)read(z),b[x][y]=z,change(1,1,n,x);
else write(t[1].d[x][y],'\n');
}
}