My Blogs
毒瘤 Ynoi。
对于加的矩形,显然是差分的拆成 $(l_1,l_2,r_2,+v)$ 和 $(r_1,l_2,r_2,-v)$ 两个线段。如果是查询的是和那是好做的,线段树历史和板子。
但是要查的是最大值,矩形查最大值因为没有可减性,不能差分,非常的困难。考虑一个弱化问题:如果是查 $3-\mathrm{side}$ 矩形的最大值,这样是好做的,扫描 $x$ 轴,$y$ 轴维护一棵线段树,支持区间加和区间查询历史最大值即可。
这启发我们把 $4-\mathrm{side}$ 矩形转化。考虑对于每个询问找到一条竖线,把询问从中间劈开,变成两个 $3-{\mathrm{side}}$ 矩形。这样仍然保留线段树维护 $y$ 轴,从中间向左做一遍,向右再做一遍就能得到答案。
处理这种问题,最常用的就是猫树分治:建一棵线段树,对于每个询问在 $x$ 坐标上找到它跨过中点的最浅的节点把询问挂在这个节点上。然后 $y$ 坐标上再用线段树区间加,查询历史最大值维护。
朴素分治
设当前处理的区间是 $x:[l,r]$(横坐标),需要知道的是两棵下标是 $y$ 坐标的线段树:
-
维护横坐标在 $[1,l-1]$ 的所有线段的和与历史最大值。
-
维护横坐标在 $[r+1,n]$ 的所有线段的和与历史最大值。
这样处理该区间的时候,先用第一棵线段树从 $l$ 向 $r$ 扫,遇到挂在该节点的询问的右端点时就更新答案。假设询问的 $x$ 区间是 $[l_i,r_i]$,这部分处理的是 $x\in[mid+1,r_i]$ 的所有位置对询问的贡献。
但是这样会有问题:希望查询的是 $x\in[mid+1,r]$ 的历史最大值,但是这样会统计上 $[1,mid]$ 的贡献。
解决方案是在 $mid+1$ 处全局加 $\mathrm{INF}$,查询的时候的真实结果是 $\mathrm{ask}-sum$,这样 $[1,mid]$ 的所有历史最大值就一定劣于 $[mid+1,r]$。
然后再用第二棵线段树从 $r$ 向 $l$ 扫一遍,处理 $x\in[l_i,mid]$ 对询问的贡献。做和上面一样的过程即可。
接下来是向左和向右递归。向左递归时,右侧线段树应当加入 $x\in[mid+1,r]$ 的所有线段。
这时就会发现需要做一个撤销或者是可持久化的过程,空间有点不优秀或者是常数比较大还不好写。
进一步优化
考虑把同层分治放到一起处理。如:
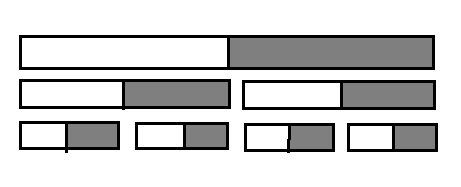
假设处理的是灰色区间,这样需要扫 $3$ 遍,第一次是第一层,第二次处理第二层,以此类推。
处理一层的时候和分治的时候差不多,从 $1$ 扫到 $n$,遇到线段就加入,遇到黑区间的左端点就全局 $+\mathrm{INF}$(查询的时候再减回来)。这样就不需要做线段树的可持久化或者是撤销。需要扫 $2\log n$ 次,每次的加矩形的复杂度是 $\mathcal O(m\log n)$,每个询问只会在某一层造成复杂度,所以总复杂度是 $\mathcal O(m\log^2 n+q\log n)$。
一些细节
可以先把 $n$ 设成 $65536$ 方便进行中点分治。把平面加矩形拆成线段的时候,需要注意不能用在 $l$ 处加,$r+1$ 处减,共用一个 vector。因为有全局加 $\mathrm{INF}$ 的操作,这样处理会有边界的问题,比如一个矩形的右端点是白区间的右端点,就会先加 $\mathrm{INF}$ 再减去该矩形右侧的线段,导致出错。
正确的姿势是开两个 vector,一个在 $l_1$ 处存 $(l_2,r_2,v)$,一个在 $r_1$ 处存 $(l_2,r_2,v)$,这样从左向右扫的时候,在一个点上的操作就是:
-
处理第一个 vector 中的加。
-
处理询问。
-
处理第二个 vector 中的减。
这样可以规避许多问题。需要开 ll,但是不要全开,容易 TLE。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
int n,m,q;
ll ans[500010];
struct Node{int l1,r1,l2,r2,id;}b[500010];
vector<tup> ve[65537],ev[65537],qu[65537];
namespace Segment
{
#define ls(p) (t[p].l+t[p].r)
#define rs(p) (ls(p)^1)
struct{int l,r;ll v,s,tg2,tg3;}t[132000];
inline void update(int p){t[p].v=max(t[ls(p)].v,t[rs(p)].v),t[p].s=max(t[ls(p)].s,t[rs(p)].s);}
inline void down(int p,ll x)
{
t[p].tg2+=x,Mmax(t[p].tg3,t[p].tg2);
t[p].v+=x,Mmax(t[p].s,t[p].v);
}
inline void down2(int p,ll x){Mmax(t[p].tg3,x+t[p].tg2),Mmax(t[p].s,t[p].v+x);}
inline void spread(int p)
{
down2(ls(p),t[p].tg3),down2(rs(p),t[p].tg3);
down(ls(p),t[p].tg2),down(rs(p),t[p].tg2);
t[p].tg2=t[p].tg3=0;
}
void build(int p,int l,int r)
{
t[p]={l,r,0,0,0,0};
if(l==r)return;
int mid=l+((r-l)>>1);
build(ls(p),l,mid),build(rs(p),mid+1,r);
}
void modify(int p,int l,int r,ll x)
{
if(l<=t[p].l&&r>=t[p].r)return down(p,x);
spread(p);
if(l<=t[ls(p)].r)modify(ls(p),l,r,x);
if(r>t[ls(p)].r)modify(rs(p),l,r,x);
update(p);
}
ll ask(int p,int l,int r)
{
if(l<=t[p].l&&r>=t[p].r)return t[p].s;
spread(p);
if(r<=t[ls(p)].r)return ask(ls(p),l,r);
if(l>t[ls(p)].r)return ask(rs(p),l,r);
return max(ask(ls(p),l,r),ask(rs(p),l,r));
}
#undef ls
#undef rs
}
using namespace Segment;
namespace Segment2
{
#define ls(p) (t2[p].l+t2[p].r)
#define rs(p) (ls(p)^1)
#define fa(p) t2[p].fa
vi T[18];
struct{int l,r,fa;vi ve;}t2[132000];
void build2(int p,int l,int r,int dp=0)
{
t2[p].l=l,t2[p].r=r,T[dp].eb(p);
if(l==r)return;
int mid=l+((r-l)>>1);
fa(ls(p))=fa(rs(p))=p;
build2(ls(p),l,mid,dp+1),build2(rs(p),mid+1,r,dp+1);
}
void push(int p,int l,int r,int id)
{
int mid=ls(p)>>1;
if((l<=mid&&mid<r)||t2[p].r-t2[p].l==1)
return t2[p].ve.eb(id),void();
if(r<=mid)return push(ls(p),l,r,id);
return push(rs(p),l,r,id);
}
}
using namespace Segment2;
const ll If=180000000000000;
inline void mian()
{
read(n,m,q),n=65536,build2(1,1,n);int l1,l2,r1,r2;ll v;
for(int i=1;i<=m;++i)
{
read(l1,l2,r1,r2,v);
ve[l1].eb(tup(l2,r2,v));
ev[r1].eb(tup(l2,r2,v));
}
for(int i=1;i<=q;++i)
{
read(b[i].l1,b[i].l2,b[i].r1,b[i].r2);
b[i].id=i,push(1,b[i].l1,b[i].r1,i);
}
for(int i=1;i<=16;++i)
{
build(1,1,n);
for(auto p:T[i-1])for(auto x:t2[p].ve)
if(b[x].r1>t[ls(p)].r)
qu[b[x].r1].eb(tup(b[x].l2,b[x].r2,x));
ll sum=0;
for(auto p:T[i])
{
if(p==rs(fa(p)))sum+=If,modify(1,1,n,If);
for(int j=t2[p].l;j<=t2[p].r;++j)
{
for(auto x:ve[j])
modify(1,x.x,x.y,x.z);
for(auto x:qu[j])
ans[x.z]=max(ans[x.z],ask(1,x.x,x.y)-sum);
for(auto x:ev[j])
modify(1,x.x,x.y,-x.z);
}
}
for(auto p:T[i-1])for(auto x:t2[p].ve)qu[b[x].r1].clear();
reverse(T[i].begin(),T[i].end());
build(1,1,n),sum=0;
for(auto p:T[i-1])for(auto x:t2[p].ve)
if(b[x].l1<=t[ls(p)].r)
qu[b[x].l1].eb(tup(b[x].l2,b[x].r2,x));
for(auto p:T[i])
{
if(p==ls(fa(p)))sum+=If,modify(1,1,n,If);
for(int j=t2[p].r;j>=t2[p].l;--j)
{
for(auto x:ev[j])modify(1,x.x,x.y,x.z);
for(auto x:qu[j])ans[x.z]=max(ans[x.z],ask(1,x.x,x.y)-sum);
for(auto x:ve[j])modify(1,x.x,x.y,-x.z);
}
}
for(auto p:T[i-1])for(auto x:t2[p].ve)qu[b[x].l1].clear();
}
for(int i=1;i<=q;++i)write(ans[i],'\n');
}