My Blogs
Day 1
$80+10+0$ 垫底。
T1
神秘题。人类智慧发现 $S$ 不会太长,生成一个 $10^6$ 的串,然后建一个类似线段树的结构。
预处理出数组 $f_{i,j}$ 表示 $T$ 的第 $i$ 位匹配一个 $S_j$ 能跳到最远的地方,可以类似倍增处理。
然后双指针在 $S$ 上跑,复杂度 $\mathcal O(n\log n)$。
T2
完全不会。
“剩余的点中选一个”很不好做,考虑对于所有排列,从前向后,如果 $p_i$ 没有被覆盖则激活 $p_i$,贡献即为激活的点的个数,因为一个方案 $[a_1,a_2\dots a_k]$ 应当被计算的次数就是它在排列中的出现次数。
然后根据期望的线性性可以拆开每个点的贡献,假设能到 $i$ 的点有 $x$ 个,$i$ 需要出现在排列的这 $x$ 个点前面,贡献为 $\frac{1}{x+1}$。所以答案即为 $\sum_{i=1}^n\frac{1}{x_i}$。
预处理每个点向上能流到哪个点,然后用支配树找到每个店被第一个完全包含的点,答案就是用向右上走到支配点的轮廓和向左上走到支配点的轮廓,这两部分对于每条竖线可以做一个数点的前缀和,然后右半部分的前缀和减去左半部分的前缀和即可。
T3
完全不会。
最多只有一个不合法,在不合法处统计不合法概率,$x_i>\sum_{j!=i}x_i$。然后 $x_i$ 和 $2^{a_i}-x_i$ 分布一样,所以就是 $\sum_{i}x_i<2^{a_i}$。
处理实数,可以拆成一个整数加一个 $[0,1]$ 的小数部分。需要处理 $n$ 个均匀分布在 $[0,1]$ 上的实数的和在 $[k,k+1]$ 的概率,转成前缀和即 $\leq k$ 的概率。
考虑积分,$\int_{0}^1 [\sum_{i}^nx_i\leq k]\text{d}x$。可以容斥,转成 $([x_1\geq 0]-[x_1\geq 1])\dots([x_n\geq 0]-[x_n\geq 1])$,然后可以拆开。所以需要处理 $\int_{0}[\sum_{i}x_i\leq k’]\text{d}x$。
Day 2
$0(100)+10+0$ 垫底,T1 莫名其妙 CE。
花 $4h$ 获得了 $10$ 昏,很厉害!
T1
打表发现满足单调性,主席树维护前缀 $k$ 小值,决策单调性分治 $\mathcal O(n\log^2n)$
T2
$\text{extremely}$ 抽象题。
考虑给定一个括号序列能否删完。Bob 的策略是简单地,一定选择最左的左括号和最右的右括号。
括号的嵌套关系可以看成是树形的结构。对于一个区间,Bob 首先要把两边匹配的括号扒完,Alice 要在这个时间内从区间内选择一个子节点(即一个匹配的括号子串)然后把别的部分删完。对树 dfs 一下即可。
结论是二分答案,假设当前为 $k$,即为判定前 $2k$ 个左括号和后 $2k$ 个右括号能不能删完即可。(?????)感觉起来是很对的。
根本没往二分答案上想。。花 4.5h 怒砍 $10$ 分,什么实力。
T3
考虑如果有一个序列,尽量把不等于 $x$ 的单独成段。
对于非 $0$ 非 $x$ 的数字可以划成一类(称为非关键值),然后分多种情况讨论,拆贡献: ######
- 序列全部是 $0,x$,因为前缀异或值和真实的每个点的值的概率是一样的,所以可以看成前缀和,然后前缀和等于 $0$ 的可以划开,所以答案是 $0$ 的个数,因为要求最后一位一定是 $0$,所以贡献是:
Jinal 2023 L
考虑 $f_{i,j}$ 为前 $i$ 个,没选 $j$ 个。枚举上一个不选的位置,可以做到 $\mathcal O(n^3)$,线段树优化到 $\mathcal O(n^2\log n)$。
可以看成操作是在结尾加入一个数,前缀加,求全局最大值。可以维护一个 $f_{i,j-1}+val(i)$ 的单调栈的差分数组,再维护一个链表表示单调栈上一段区间的左右两个,并查集维护每个点在哪个单调栈的区间上,如果加到差分小于 $0$ 了就把下一段删掉和当前区间合并,复杂度变为 $\mathcal O(n^2\alpha(n))$。
Hangzhou 2022 L
给定 $S,T$ 串,求 $S$ 中有多少子串满足和 $T$ 串的编辑距离分别为 $[0,k]$。
考虑传统求编辑距离,是 $f_{i,j}$ 表示 $S[1,i]$ 和 $T[1,j]$ 的编辑距离,因为要求答案不超过 $k$,所以只有 $\mathcal O(k)$ 条对角线的 DP 值是有用的。
对于一条斜线,可以发现 DP 值是单调递增的,可以值域下标互换,设 $f_{i,j}$ 为修改 $i$ 个字符,在第 $j$ 条斜线上的最远点是 $f_{i,j}$(即 $S[1,x]$ 匹配上 $T[1,x+j]$) 最大的 $x$,需要求 LCP,后缀数组转成 RMQ 即可。对于每个 $S$ 的后缀求一遍,复杂度 $\mathcal O(nk^2)$。
CF1930G
考虑对着值域 DP,$f_i$ 表示当前 $i$ 是 dfs 序列中的最后一个并且是前缀最大值是 $i$ 的方案数,则 $i$ 转移到 $j$ 有两种情况:
-
$i$ 是 $j$ 的祖先,则需要 $(i,j)$ 的链上不能有 $>i$ 的点。
-
$i$ 不是 $j$ 的祖先,则需要 $i$ 是 $lca_i$ 子树内的最大值且 $(lca,j)$ 的链上不能有 $>i$ 的点。
考虑把可能是前缀最大值的点设为关键点,只考虑关键点。则第一种转移一定是由最近的关键点祖先转移得来。
第二种关键点一定是由编号在 $[fa_j,j]$ 之间的点转移而来。所以就是 $j$ 到根的链上的所有叶子中编号在 $[fa_j,j]$ 之间的点,可以遍历这棵树的结构,然后树状数组维护当前根链的所有叶子的编号的方案数和。注意到一个儿子只有叶子才能发生第二种转移走出去,所以可以直接 dfs 过程中按照最大的叶子从小到大遍历儿子,退出来的时候把贡献去掉,只保留子树内最大的叶子的贡献,复杂度是 $\mathcal O(n\log n)$。
UR #26 C 铁轨回收
考虑最后是一个树形的结构,从后向前做(?)。
Day 3
组合数学。
P0
求把 $n$ 划分成的有序序列包含偶数个偶数的方案数。
如果没有限制,就是 $2^{n-1}$。然后考虑证明偶数个偶数和奇数个偶数相等。
构造双射,如果第一项是 $1$ 就把 $1,2$ 项合并,否则把第 $1$ 项 $a_1$ 拆成 $1$ 和 $a_1-1$,然后这样奇偶性一定是会变的,所以一一对应。
P1
证明:
\[\sum_{k=0}^m\binom{m+k}{k}2^{-k}=2^m\]变形一下
\[\sum_{k=0}^m\binom{m+k}{k}2^{m-k}=2^{2m}\]考虑一个长为 $2m$ 的 $01$ 序列,上式即为在枚举第 $m+1$ 个 $1$ 在 $m+k+1$ 这个位置,左边就是选择 $k$ 个 $0$,然后右边是随便选,和原序列一一对应。
P2
证明
\[\sum_{k=0}^n\binom{2k}{k}\binom{2(n-k)}{2k}=4^n\]考虑一个 $2n\times2n$ 的坐标系,从 $(0,0)$ 开始走到 $y=4n-x$ 的方案数。上式枚举最后一次和 $y=x$ 的交点 $(k,k)$,后面是
Day 3
$100+36(56)+40$ 垫底。
T1
抽象打表找规律过了。
正解组合意义,整理式子得:
\[f(n)=\sum_{k=0}^n2^{n-k}\sum_{m=0}^k\binom k m\binom {k-m}{\lfloor\frac{k-m}{2}\rfloor}2^m\]设 $S=[2n+1]$,钦定其中 $1,2$ 匹配,$3,4$ 匹配$\dots$,$2n+1$ 没有匹配。
对于 $x\geq 2n$ 的 $x$ 的匹配对象设 $m(x)$。
选取 $T\subseteq S$ 使得 $\lvert T\rvert=n$ 的方案是 $\binom{2n+1}{n}$。
对于每种方案,设 $R={x\vert x\in T,x\ne 2n+1,m(x)\notin T}$,设 $k=\lvert R\rvert$。
确定了 $k$ 之后,可以得到 $T$ 中有 $\lfloor\frac{n-k}2\rfloor$ 对匹配,这样得到了$\binom{2n+1}{n}$组合意义:
先确定 $n$ 对匹配中,$k$ 对匹配恰好被选进 $T$ 集一个,并且决定哪个被选入,方案数是 $\binom n k 2^k$。
剩下还需要选恰好 $\lfloor\frac {n-k}2\rfloor$ 对匹配,方案数是 $\binom{n-k}{\lfloor\frac{n-k}2\rfloor}$。
根据 $n-k$ 的奇偶性可以确定 $2n+1$ 选不选,这样就得到了一个大小为 $n$ 的集合 $T$。
T2
逆天,不会斯特林数。会下降幂的 dp 最后没发现系数是斯特林数。。。
考虑 $m=1$ 的情况,对于一个排列,表示一种方案中第一次出现的顺序,拆每个数的贡献。最后一个数的贡献一定是 $1$,前面的数的贡献的话,假设是第 $i$ 位数的贡献,则 $p_i,p_{i+1}$ 之间有 $\frac{i-1}n$ 个数可以任意选出现任意次,即 $\sum_{len=0}^{\infin}(\frac{i-1}n)^{len}=F(\frac{i-1}n)$,其中 $F(i)=\frac{1}{1-i}$。然后同理的 $p_{i+1},p_{i+2}$ 之间有 $\frac{i}n$ 个数可以任意出现任意次,以此类推。
然后 $i$ 前面的数不会被影响,$p_j,p_j+1(j<i)$ 的间隔中可以出现 $\frac{j}{n}$ 种,所以是 $F(\frac j n)$。最终得到 $i<n,i$ 的贡献是 $\frac {n!}{n^n}\sum_{j=1}^{n-1}F(\frac{j-[j>i]}n)$。前缀后缀和一下即可。
扩展到 $m>1$ 的情况,就是设 $f_{i,j}$ 表示排列的前 $i$ 个数,有 $j$ 个钦定为只出现一次,转移是:
\[\begin{aligned} f_{i+1,j}&\rightarrow f_{i+j,j}+f_{i,j}F(\frac{i-j}{n})\\ f_{i+1,j+1}&\rightarrow f_{i+j,j+1}+f_{i,j}F(\frac{i-j}{n})(j+1)\\ \end{aligned}\]处理这部分的复杂度是 $\mathcal O(nm)$ 的。这样因为没有处理 $i,i$ 之间的贡献,所以算出来的是 $E(x^{\underline k})$。要求的是 $E(x^k)$,就用斯特林数转成下降幂:
\[E(x^k)=\sum_{i=0}^kS(k,i)E(x^{\underline i})\]这样就做完了。不要把求逆元写进 dp 里否则复杂度退化,需要卡卡常,比如把 dp 过程中的 $j+1$ 放到最后乘,$n!$ 和 $\frac 1{n^n}$ 也放到最后乘,加法不要取模,这样就能较快的通过。
T3
神秘题。
首先若 $[1,m]$ 非降,一定是不断操作 $[1,m]$ 直到第一个被完全删掉,这样操作直到非不降。此时设 $i$ 表示满足 $[1,i]$ 非降的最大的 $i$。
因为 $a_i>a_i+1$,所以称 $(i,i+1)$ 是一个 $\text{gap}$。对于一个 $\text{gap}$,则一定有 $a_i-a_{i+1}$ 个操作区间以 $i$ 为结尾。以 $\text{gap}$ 结尾的操作的起始位置自然是越靠左越好。
因为第一个 $\text{gap}$ 前面本身是单增的,所以存在合法方案使得 $\text{gap}$ 消除并且满足单增到下一个 $\text{gap}$。
这里有一个很强的性质:先把 $\text{gap}$ 全部消掉,操作选取 $[i-m+1,i]$。虽然这样可能会减到负数,但是是无所谓的,因为知道有合法方案。
这样就转化成把区间内全部删成 $\leq 0$ 的数,可以再转化成选取若干个数,使得数与数之间的最小间隔不超过 $m$ 并且选出的数权值和最大。
但是这样对于区间有一个问题:可能会操作 $r$ 右边的 $\text{gap}$ 时操作到了 $r$,不好统计答案。但是有一个很聪明的解决办法:只统计 $[l,r-1]$ 间的 $\text{gap}$,最后删到 $[r-m+1,r]$ 的时候一定是递增的,所以最后需要的权值就是 $a_r$。这样一个区间的答案就是:$[l,r-1]$ 间的 $\text{gap}$,把 $[l,r-m]$ 间的数删成非正,再加上 $a_r$。
考虑如何统计答案。信息没有结合律,看起来不太能 $\text{polylog}$,直接考虑对于 $m$ 大小分治。
先判掉询问区间较小的,暴力做 DP 即可。
对于 $m$ 较小的部分,因为没有结合律,直接考虑中点分治。对于跨过这个中点的询问,左右两边选的第一个数的间隔一定 $=m-1$。所以从 $[mid-m+1,m]$ 向左预处理再从 $[mid,mid+m-1]$ 向右预处理,这样询问就是两个点拼起来。这部分复杂度是 $\mathcal O(nm\log n)$
对于 $m$ 较大的部分,相对复杂一些。考虑对于整个序列长度为 $m$ 分块。
如果询问和某个块有交并且没有再这个块里选东西,那可以直接预处理块两端到序列最左最右两端的 DP 然后拼起来。
对于再所有块里都选的部分,考虑把每一块“摞”起来。
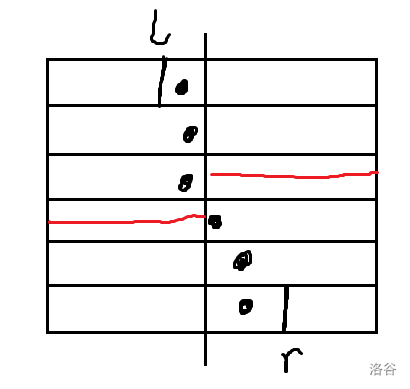
容易发现因为每一块都有选点,所以选的点一定越来越靠右。再次考虑进行中点分治。
如果选的点跨过了中线,则一定有红色的线对应的区间没有选点,可以仿照上一个做法。
Day 5
$0(40)+100+40$,比垫底好一些,T1 又是神秘 CE,怎么会事呢。。
T1
我是弱智。
可以看成是匹配问题。设 $f_{i,S}$ 表示前 $i$ 行,和 $S$ 中的方案匹配合法概率,其中 $S$ 是一个 $\binom{n}{i}$ 位的二进制数。(匹配上的理解是前 $i$ 个点,$S$ 是一个子集族表示 $[1,i]$ 匹配 $S$ 中所有集合合法)经过搜索发现状态只有几万个,然后就赢麻了。预处理状态间的转移,然后 DP 的复杂度就是 $\mathcal O(n2^nT)$,$T$ 为状态数。
以为状态数会炸,根本没有往这想/ll。
神 Mikefeng队长 的做法:还是转成匹配,考虑 $\text{Hall}$ 定理。考虑统计不合法的图的个数。
直接做很大的问题是会算重。考虑在某个特定位置进行统计答案:左侧点减去右侧相邻点集大小最大的子集处进行统计,如果有多个差相同的则在左侧点集最小处统计。
可以证明这样一个图只会被统计一次,因为如果存在两个大小相同的集合 $S,T$ 满足 $\lvert S\rvert-\lvert N(S)\rvert=\lvert T\rvert-\lvert N(T)\rvert$,则 $N(S\cap T)=N(S)\cap N(T)$,$N(S\cup T)=N(S)\cup N(T)$。这样不论 $ST$ 有没有交,一定有 $S\cup T$ 更优或者 $S\cap T$ 不劣而且其大小更小,所以满足条件的只有一种。
所以需要枚举所有左侧点的子集 $S$ 和右侧点的子集 $S1$,求 $<S,S1>$ 为最小不合法 $\text{Hall}$ 定理条件的 $01$ 矩阵出现概率。下设这个值为 $f_{S,S1}$
可以先假设 $f_{S,S1}$ 为 $N(S)=S1$ 的 $01$ 矩阵出现概率,减去更小的不合法矩阵出现概率。假设这个更小的为 $T,T1$。
若 $S,T$ 无交。则 $T\cap S$ 是比 $S,T$ 都更小的不合法 $\text{Hall}$ 定理子集。所以 $T$ 不合法,无需考虑。
若 $S,T$ 有交,但不包含。则 $T\cup S$ 又是比 $S,T$ 更小的不合法 $\text{Hall}$ 定理子集。所以 $T$ 也不合法,也无需考虑。
这样只剩最后一种情况:$T\subseteq S$ 或者 $S\subseteq T$。
如果 $T\subseteq S$,则有 $\lvert T\rvert-\lvert T1\rvert\geq \lvert S\rvert-\lvert S1\rvert$,如果 $S\subseteq T$,则有 $\lvert T\rvert-\lvert T1\rvert>\lvert S\rvert-\lvert S1\rvert$,注意取等不同。
所以可以按照第一关键字是 $\lvert S\rvert-\lvert S1\rvert$ 从小到大,然后第二关键字是 $\lvert S\rvert$ 从小到大的顺序递推,这样若 $T\subseteq S$ 就使用第一关键字小于当前的 $T$ 去更新,若相反则用第一关键字相同,第二关键字更小的 $T$ 去更新。
设 $f_{S,S1}$ 表示 $(S,S1)$ 是 $S$ 子集内最小不合法 $\text{Hall}$ 定理子集的概率。$g_{S,S1}$ 为 $(S,S1)$ 内所有子集合法的概率。这样不用考虑超集的问题。
需要预处理的有 $val1{i,S}$ 表示点 $i$ 全部连上 $S$ 中的点的概率,$val2{i,S}$ 表示 $i$ 和 $S$ 中的点没有连边的概率,$h1{S,S1}$ 表示 $S1$ 中每一个点都至少在 $S$ 中有边的概率,$h2{S,S1}$ 表示 $S,S1$ 间一条边也没有的概率。设 $i$ 为 $S$ 的最高位,转移方程为:
\[\begin{aligned} h1_{S,S1}&=\sum_{i\in S1}(1-\sum_{j\in S}(1-a_{j,i}))\\ h2_{S,S1}&=h2_{S\oplus 2^i,S1}\times val2_{i,S1} \end{aligned}\]一式是枚举最后一位连上了 $T1$,然后 $S$ 中除去 $i$ 的其他位连上了 $T$。
然后再对 $f,g$ 进行 DP,转移方程为
\[f_{S,S1}=h1_{S,S1}-\sum_{T\subseteq S}^{\lvert T\rvert-\lvert T1\rvert\geq\lvert S\rvert-\lvert S1\rvert}f_{T,T1}\times h2_{T,S1\oplus T1}\times g_{S\oplus T,S1\oplus T1}\]要求 $\lvert S\rvert>\lvert S1\rvert$。上式的意义式枚举 $T,T1$ 比 $S,S1$ 优秀,然后剩余部分是合法的因为不合法的方案和 $T,T1$ 是一一对应的。上面有结论一个匹配只有一个最优秀的不合法的,除去这个最优秀的不合法的剩下的就是合法的。
因为 $f_{T,T1}$ 只保证了 $(T,T1)$ 是图的 $(T,T1)$ 子集中最优秀的不合法方案,所以 $T$ 不能向其他点连边。
\[g_{S,S1}=h1_{S,S1}-\sum_{T\subseteq S}^{\lvert T\rvert-\lvert T1\rvert\geq\lvert S\rvert-\lvert S1\rvert}f_{T,T1}\times h2_{T,S1\oplus T1}\times g_{S\oplus T,S1\oplus T1}\]唯一的区别是要求 $\lvert S\rvert\leq \lvert S1\rvert$。意义就是枚举最优秀的不合法方案减掉。最后 $g_{2^n-1,2^n-1}$ 就是答案。
T2
比较简单的题,场上连续发生模数写错和组合数越界的弱智错误。。。
设 $f_{i,j}$ 表示 $i$ 子树内再从父亲上面扔进来 $j$ 的方案数,转移比较麻烦但是没啥思维难度,懒得抄了,复杂度大概是树形背包?。
T3
神秘题,暴力费用流 $30$,改成邻接矩阵 $40$,场上可能会 $60$ 但是写不出来/ll/ll。
曼哈顿距离转切比雪夫距离,$\lvert x-x_i\rvert+\lvert y-y_i\rvert$
例1
求区间所有子区间的 $\text{LCA}$ 编号之和。
对于一个子树,它内部的编号是若干个连续段。
$[l,r]$ 内的 $\text{LCA}$ 如果是 $u$,则编号对应的连续段应当包含 $[l,r]$ 并且 $u$ 子树内其编号不连续。设有一个 $l,r$ 平面,然后把子树内编号连续段合并的时候会产生一个新的矩形,这样就是若干个矩形查矩形和,线段树历史和维护。
这里的合并是编号恰好连续,即 $[a,b]$ 和 $[b+1,c]$,因为只会合并 $n-1$ 次,所以复杂度 $\mathcal O(n\log n)$。
例2
有 $n$ 个人,每个人有一个六面骰子,面上的数是 $A_{i,1},A_{n,2}\dots A_{n,6}$。你可以花 $-ab$ 的代价定制一个两面权值为 $a,b$ 的硬币。
会进行一次游戏:你扔硬币,其他 $n$ 个人扔骰子,若你的权值 $\geq$ 第 $i$ 个人的权值,则获得 $K_i$ 的收益,求最大期望收益减代价。
首先每个人显然独立,如果 $a>A_{n_i}$ 则获得 $\frac{k_i}{12}$ 的期望收益。问题可以看成一个全是 $-1$ 的平面上,横轴和纵轴有 $6n$ 个分隔点,求最大二维前缀和。可以从左向右扫描线过程中维护纵轴的 $6n$ 个点的凸包,每次斜率 $+1$,或者全局加一个值。
例3
定义好看数 $x$ 为 $x(10^k-1)$ 的十进制表示下没有数码 $b$,求第 $m$ 个好看数。
$m\leq 10^16,k\leq 16$。
可以不从 $x$ 出发从 $(10^k-1)$ 的倍数出发。感觉答案不会很大。因为要求第 $m$ 个,考虑从前向后确定。
一个神奇结论是 $10^k-1$ 的倍数的充要条件是每 $k$ 位分一段之后求和是 $10^k-1$ 的倍数。这样就可以分段一起 DP,就是类似有 $\lfloor\frac{n}{k}\rfloor$ 个指针,每次一起向左移动一位,也可以理解为每 $k$ 位分段之后摞在一起做一个竖式加法,可以设 $f_{i,j}$ 表示考虑了后 $i$ 位当前位有 $j$ 个进位,转移比较简单。
Day 6
破防了,$80(100)+30+20(65)$,挂了一万分,不拍导致的。
T1
离线,把两个串最后拼起来,求出 $\text{SA}$,每个询问在 $\text{SA}$ 中的位置左右二分到最远的距离,因为有对 $A$ 的区间限制,所以转化成二维数点,数 $A$ 匹配的左端点个数,扫描线树状数组维护。
T2
呜呜呜我不会我不会我不会。。。
为什么都会。。。
一个合法的层级值唯一对应一种点分树。可以归纳证明:找到全局最小值(如果有多个全局最小值则不合法),然后删去最小值去处理剩下的子树。
层级值合法的充要条件是两个值相等的点之间存在层级值比它小的点。考虑如果现在有一棵标好层级值的树如何 $\text{DFS}$ 进行判定。子树内可能和外部点构成非法的匹配的点只有从 $i$ 向下 $\text{DFS}$ 走到的前缀最小值点。
所以需要状压 $\text{DP}$ 值域,设 $f_{i,j,S}$ 表示 $i$ 子树内,$h_i=j$,子树内前缀最小值有无的一个 $k$ 位二进制数 $S$。转移需要子集卷积(因为合并子树的时候需要保证 $S$ 不交。)
T3
挂挂挂。
显然可以先建出 $\text{Kruskal}$ 重构树(最小生成树)。然后如果枚举 $A$ 树最大值,$A$ 最大值递增的过程中 $B$ 最大值应当是非增的,类似一个双指针的结构。需要在 $A$ 中加边,$B$ 中删或者撤销边。
$A\cap B$ 的限制不好做,转成 $\lvert A\rvert+\lvert B\rvert-\lvert A\cup B\rvert$,因为与的限制有传递性,可以把图划分成若干个等价类,等价类集合内部的点 $AB$ 联通。
$A$ 中的加边相对好维护,但是 $B$ 中删很难。所以考虑等价类一定是 $B$ 最小生成树上的连通块,删边之后如果该边两端原来是一个连通块,就分裂。
考虑在 $\text{Kruskal}$ 重构树上进行这一个过程:不断尝试删去 $B$ 中最大的边就是找到当前最大的节点,然后把挂在该节点上的等价类分裂到两个子树内,启发式分裂的复杂度是对的。
CF1943D2
做过。
另一个做法:考虑如果 $a_{i-1}>a_i$ 则 $i+1$ 填什么数 $i$ 都合法,所以这种情况 $i+1$ 可以填一个 $<a_i$ 的,也可以填 $>a_i$ 的。
对于 $a_i>a_{i-1}$ 的情况,因为我们要压状态,所以只能记一个 $[0,k]$ 的信息。这种情况填 $>a_i$ 的情况一定合法,然后 $<a_i$ 不知道。所以考虑在 $i-1$ 的时候后面直接接两个数然后钦定合法,系数可以直接算,这样问题就解决了。再开一维 $01$ 表示 $a_i,a_{i-1}$ 大小关系。
CF1270G
做过。
考虑乱跳,值域是 $n^2$ 的。
考虑正的向左跳,负的向右跳,值域是 $2n$ 的。
但是还不够,希望用抽屉原理把值域限制到 $n$。
假设现在值是 $V$。假设钦定的值域范围就是 $[1,n]$,那要求 $1\leq V+a_i\leq n$,变形,$1-V\leq a_i\leq n-V$,所以 $V=n-i+1$ 时恰好满足题目限制,所以可以这样跳,一定会有两个相同的位置的值相同(因为有 $n+1$ 个数,第 $1$ 个数是 $0$,剩下的是被限制在值域里的数。)
Day 7
$100+15+50$
T2 没写完。
T1
$\text{4-SAT}$ 不可做,可以尽量让一个点成为 $C,D$,然后剩下的就是 $A,B$。
如果有 $1$ 入边一定不是 $C$,$1$ 出边一定不是 $D$。对于 $C$,其 $0$ 出边一定是 $C$,$D$ 的 $0$ 入边一定是 $D$。把可能是 $CD$ 的点单独拎出来跑两边拓扑排序确定可以是 $CD$ 的,然后剩下的跑一边二分图染色。
T2
唐。
判掉 $m=n$ 和 $m=n-1$。打表发现如果 $m$ 是奇数一定合法,如果 $m$ 是偶数,则排列的逆序对数必须是偶的,因为操作不改变逆序对的奇偶性。
发现可以通过 $\mathcal O(1)$ 次操作交换 $i,i+1$ 和 $i+1,i+2$,所以从前向后暴力,假设要交换 $a,b$,就把 $a,b$ 移到 $n-3,n-2$ 的位置然后交换。对于奇排列,先用 $\mathcal O(m)$ 次操作交换最后两个数把它变成偶的。细节很多,导致场上没写完。
T3
Day 8
T1
为什么不会呢。
先考虑判定,存在一位是只有该数为 $0$,记为独特位,但是问题在于一个一个加数之后不能立刻知道是不是独特位。然后有 DP 套 DP,记连通性。
然后可以发现极小正交子集是没有无独特位元素的正交子集,可以进行容斥。场上大概是想到了这一步,但是没想到容斥怎么计数。
可以转为计数 $T\subseteq S$ 且 $S$ 是正交子集,$T$ 可以是空集并且 $T$ 中元素都无独特位,容斥系数是 $(-1)^{\lvert T\rvert}$。这样求和之后极小的系数和是 $1$,其余的系数是 $0$。
所以设 $f_{i,S}$ 是考虑前 $i$ 个数,位状态是 $S$ 的带容斥系数的方案数之和。其中 $S$ 每一位有 $3$ 中状态:
-
$S$ 中按位与是 $1$。
-
$S$ 中按位与是 $0$ 并且还存在一个 $T$ 内的元素是这一位唯一的 $0$。
-
$S$ 中按位与是 $0$ 并且不存在一个 $T$ 内的元素是这一位唯一的 $0$。
转移 $\mathcal O(1)$,总复杂度 $\mathcal O(Tn3^9)$。
T2
简单题,用全局减去不相交的。设当前的询问路径是 $A$,权值路径是 $B$,有两种情况:
-
$B$ 的两个端点在 $A$ 的某个节点的相同子树里。该相同子树不能是 $A$ 中的节点。
-
$B$ 两个端点都在 $A$ 外部。
第二种情况就是总的减去至少有一个在内部,树上差分。第一种把权值放到 $\text{LCA}$ 上就是子树和。因为不能是 $A$ 中的节点,所以要在加回来一部分。复杂度 $\mathcal O(n\log n)$,瓶颈在于求 $\text{LCA}$。
T3
不会。为什么都(zzk)会。
假设大佬的码力是 $x+y$,其他人是 $x$,其中 $x,y>0$
实际上是需要设计一个变换,有 $n$ 中可能的输入:
$x+y,x,x\dots$
$x,x+y,x\dots$
$\dots$
需要保证每种输入对应的输出不同。
考虑记录一个长度为 $m$ 的序列 $C$,第 $i$ 项为 $S_iA-S_iB$,如果一个序列是另一个序列的倍数,那这两个序列应当对应同一个人是大佬。所以是在求 $\lvert {yC\vert y\in R^+,\forall i,C_i\in[-k,k]}\rvert$。可以全部除最大公约数然后变成长度位 $m$ 的序列全局 $\gcd$ 为 $1$。可以枚举 $\gcd$ 莫反。