Day 1
1. 星辰
对合排列的限制是假的,因为 $P$ 的逆序对等于 $P$ 的逆排列的逆序对,非对合排列之间构成双射。
考虑生成函数:
\[\begin{aligned} F(x)&=\prod_{i=0}^{n-1}(\sum_{j=0}^i x_j)\\ &=\prod_{i=1}^n\frac{1-x^i}{1-x}\\ &=\frac{1}{(1-x)^n}\prod_{i=1}^n(1-x^i) \end{aligned}\]可以初始设 $f_{i}=\binom{i+n-1}{n-1}=[(n-1)\subseteq(i+n-1)]$,然后 bitset 优化 DP。
2. 珍珠
懒得喷。
3. 混凝土
对于单组询问,首先计算 $f_{d}$ 表示 $d\vert \gcd$ 的答案,对 $f$ 做一遍狄利克雷差分(莫反)就是 $d=\gcd$ 的答案。枚举 $d$ 之后,问题变成选 $n$ 个 $\lfloor\frac m d\rfloor$ 以下的数,要求 $\mathrm{lcm}>\lceil\frac A d\rceil$ 。上取整变成全体减下取整方便一点。然后再枚举 $\mathrm{lcm}\vert v$,则满足:
\[\begin{aligned} \sum_{d\vert v}c_d&=\sigma(v)^n\\ c_v&=\sum_{d\vert v}\sigma(d)^n \end{aligned}\]$c_i$ 表示 $\mathrm{lcm}$ 为 $i$ 的答案。
\[f_d=\binom{\lfloor\frac m d\rfloor+1}{2}^n-\sum_{k=1}^{\lfloor\frac{A-1}{d}\rfloor}k^nc_k\\\]答案即为 $\sum_{i=1}^B\sum_{i\vert j}\mu(\frac j i)f_j=\sum_{i=1}^Bf_i\sum_{j=1}$。枚举 $B$,$f_j$ 的贡献系数变化次数是 $\mathcal O(m\log m)$ 的。树状数组维护区间系数和,查询直接暴力整除分块查,复杂度是 $\mathcal O(m\log^2 m+T\sqrt m\log m)$。看不懂 $\mathcal O((m+T)\log^2 m)$ 咋做。
Day 2
1. 三元组统计
$\mathrm{min-max}$ 荣斥?比较神奇:
\[\begin{aligned} &\max\{a_i-a_j,b_i-b_j,c_i-c_j\}-\min\{a_i-a_j,b_i-b_j,c_i-c_j\}\\ =&(a_i-a_j)+(b_i-b_j)+(c_i-c_j)\\ &-\min\{a_i-a_j,b_i-b_j\}-\min\{a_i-a_j,c_i-c_j\}-\min\{b_i-b_j,c_i-c_j\}\\ &+\min\{a_i-a_j,b_i-b_j,c_i-c_j\}-\min\{a_i-a_j,b_i-b_j,c_i-c_j\}\\ =&(a_i-a_j)+(b_i-b_j)+(c_i-c_j)\\ &-\min\{a_i-a_j,b_i-b_j\}-\min\{a_i-a_j,c_i-c_j\}-\min\{b_i-b_j,c_i-c_j\}\\ \end{aligned}\]二维偏序。
2. 烤鸭店
简单 DP。$f_{i,j}$ 表示 $i$ 的收益钦定为 $j$,初值是 $f_{i,0}=0,f_{i,j}=v_{j-1}-w_i$。转移:
\[f_{i,j}\leftarrow + \max\{f_{to,j-1},f_{to,j},f_{to,j+1}\}\]3. 生成数计数
离散对数转成加法。首先要求 $\prod (1+x^i)\pmod {x^{\varphi(p)}-1}$。可以直接 bitset 做到 $\mathcal O(\frac{nm}{w})$。有高妙的均摊做法:
维护一棵线段树或树状数组来求区间哈希值。每次可以看成是一个数组平移若干位和原来的数组或上去。不断找到新数组和原来数组不一样的第一个地方,尝试对原数组进行更新。
如果找到了原来是 $0$ 现在是 $1$ 的地方,势能减小 $1$。如果找到了原来是 $1$ 现在是 $0$ 的地方,可以证明这两种形态是一一对应的。所以总复杂度就是对的,是 $\mathcal O(p\log^2 p)$。
最后还要做一次 NTT。
Day 3
1. 矩阵计数
序列顺序无关,从小到大排序,则矩阵的形态:
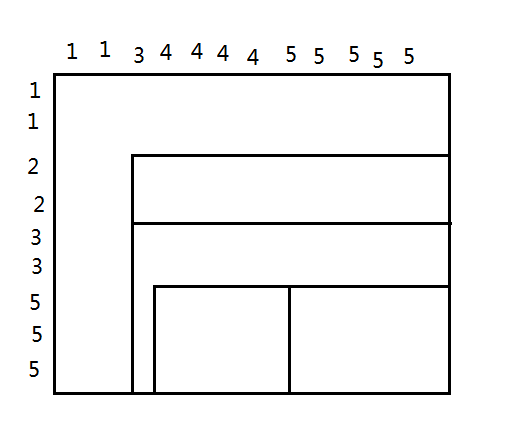
每个 L 形里面的大小限制相同。分开计算。对行,列进行荣斥:
暴力计算复杂度就是对的。
2. 树上逆序对问题
转成 $\frac{l(l-1)}{2}-\sum_{i}\frac{c_i(c_i-1)}{2}$,$c_i$ 表示颜色 $i$ 的出现次数。可以树上莫队。
3. 背包装物品
考虑生成函数:
\[\begin{aligned} F(x)&=\frac{1}{(1-x)^n}\frac{1}{(1-x^2)^m}\\ &=\frac{1}{(1-x)^{n+m}}\frac{1}{(1+x)^m}\\ &=\sum_{i\geq 0}\sum_{j\geq 0}\binom{n+m-1+i}{i}x^i\binom{m-1+j}{j}(-1)^jx^j\\ &=\sum_{k\geq 0}x^k\sum_{0\leq j \leq k}\binom{n-m-1+k-j}{n-m-1}(-1)^j\binom{m-1+j}{m-1}\\ \end{aligned}\]不考虑了。代数推导天地灭,组合意义保平安。代数推导天地灭,组合意义保平安。代数推导天地灭,组合意义保平安。代数推导天地灭,组合意义保平安。代数推导天地灭,组合意义保平安。代数推导天地灭,组合意义保平安。代数推导天地灭,组合意义保平安。代数推导天地灭,组合意义保平安。代数推导天地灭,组合意义保平安。代数推导天地灭,组合意义保平安。
枚举有多少个体积为 $1$ 的物品选了奇数个。选了奇数个的就先强制选一个,然后全部当成偶数:
\[\sum_{i=0}^n\binom{n}{i}\binom{\frac{k-i} 2+n+m-1}{n+m-1}\]组合数用 Lucas 定理算。
Day 4
1. Boring Queries
这下记住了。min 和 max 排序,xor 拆位算,集合大小看成选 $1$。每一位从前向后 DP,$f_{i,0/1,0/1}$ 表示前 $i$ 个中是否已经选了,异或值是 $0/1$ 的最小值权值和。$\mathcal O(1)$ 转移。
2. 石子游戏
取的一定是一个区间。一定是 $[i,i+k-1]$ 或者 $[i-k+1,i]$。判掉 $k=1$。
先找到 $[i,i+k-1]$ 区间最大值 $x$。如果 $P<x$ 则一定不合法。如果 $P>x$ 则要求 $a_{i+k}>x$。
如果 $P=x$,再找到区间次大值,小于 $x$ 则合法,否则不合法。
3. 树上的问题
平衡树维护点权,断边用启发式分裂。是不是过不去啊。正解是线段树维护一个并查集。
Day 5
1. 数列题
根号分治优化 DP。区间加可以差分。
2. 数论题
神奇题目。首先考虑没有删除一个数怎么做。
核心性质是 $i^t\times j^t=(ij)^t$。所以把 $a_i$ 和其他所有数相乘,看得到的数在不在序列中。如果 $a_i$ 在序列中的数大于 $\sqrt n$ 个,则 $a_i=c^t$ 的 $c<\sqrt n$,可以确定。然后跑一遍 BSGS 就能求出来 $t$。
问题是如何找到一个 $c$ 比较小的 $a_i$。看 $a_i\times a_i$ 是否在序列里即可。
删掉了一个数之后 $c$ 可能会变成 $c+1,c+2$。都 chk 一遍就行了。
3. 鸽子湖
有点唐了。首先设 $p_{u,v}$ 表示从点 $u$ 走到点 $v$ 的最大权的最小值。求 $p$ 可以用 Kruskal 重构树。
如果 $p_{u,v}>h_u$,则 $u,v$ 连通,$h_u=h_v$。其余的没有影响。
$p_{u,v}>h_u$ 的点在 Kruskal 重构树上是一个子树,可以倍增找出。接下来对 $h_u$ 和 $h’$ 的大小分类讨论。
- $h_u<h’$。区间推平。
- $h_u<h’$,此时 $h_v$ 应变成 $\max (h’,p_{u,v})$。
可以打 tag $(x,y)$ 表示 $h_v=\max(x,h_{y,v})$,tag 是区间覆盖的。线段树维护。
Day 6
1. 海棠喵的传送
首先是同时传送,所以每个人的坐标都形如:$2c_1-2c_2+2c_3\dots \pm x$ 且 $x$ 的正负号相同。把 $c$ 全体 $\times 2$,列出等式发现只和 $A-B$ 有关。
令 $d$ 表示第一个人选择的操作序列,$c$ 表示第二个人选择的操作序列。则需要满足 $A-B=\sum_{i=1}^k (-1)^i(c_i-d_i)$。然后发现 $(-1)^i$ 是假的,因为可以通过交换 $c_i$ 和 $d_i$ 来得到自己想要的正负号。
考虑一个暴力,二分答案,对于每个点找出能和他同时进行的点。这样会得到一些数,对其求 $\gcd$,检查 $\gcd$ 是否是 $A-B$ 的因数即可。复杂度 $\mathcal O(qn^2\log V)$。要求 $\gcd_{i=l}^r{a_i-x}$,邻项相减,变成 $\gcd(a_l-x,\gcd_{i=l+1}^r{a_i-a_{i-1}})$,预处理一下可以做到 $\mathcal O(qn\log V)$。
再大眼观察一下,发现只有相邻两个数是有用的。。。整体二分,线段树维护区间 $\gcd$。
2. 海棠喵的集合
困难。首先考虑怎么判断一个 $01$ 串是否合法。可以进行两种操作:
- 选择一个最大的 $k$ 满足 $01$ 都是 $k$ 个相同的一段,然后把一段缩成一个。
- 选择相邻两个距离最近的 $1$,然后把 $1000\dots$ 变成一个 $1$。
两种操作轮流操作。容易发现一个 $01$ 序列对应唯一的操作序列,构成单射。
对于一个操作序列,可以通过这样的方式构造一个合法 $01$ 序列:初始化第一位是 $1$,然后缩序列的时候把后面的位都设成 $1$,可以倒退出一个唯一的 $01$ 序列,所以两者构成双射。
计 $(x,y)$ 表示序列中 $1$ 的个数和序列长度。两种操作分别是变成 $(\frac x k,\frac y k)$ 和 $(x,\frac y k)$。可以看成是初始 $(a,b)=(1,1)$,每次把 $a$ 或 $b$ 乘一个数,相邻两次乘的不同,最后变成 $(n,m)$。把 $n$ 因数分解后,看成是有 $k$ 种球,每个有 $a_k$ 个,放到 $[1,\sum a]$ 个盒子里的方案数。对 $n,m$ 分别求解之后可以对应位,对应位差一相乘求和就是答案。
荣斥计算:$f_i$ 是 $i$ 个盒子可以为空的答案,$g_i$ 是 $i$ 个非空盒子的答案。
\[\begin{aligned} f_i&=\sum_{j=1}^k \binom{a_j+i-1}{i-1}\\ f_i&=\sum_{j=0}^i\binom{i}{j}g_j\\ g_i&=\sum_{j=0}^i\binom{i}{j}(-1)^{i-j}f_j \end{aligned}\]只有 $\sqrt k$ 种本质不同的 $a_i$,求 $f$ 可以暴力 $\mathcal O(n\sqrt n)$ 求,反演回 $g$ 需要 FFT。
3. 海棠喵的括号
$23$ 操作的执行是唯一确定的,只需要保证序列左右括号相等。
接下来不断做这个过程,就是最小答案:左括号看成 $+1$,右括号看成 $-1$,找到第一个前缀和 $<0$ 的位置,从这个位置之后找到第一个左括号,把左括号移过来。暴力做可以做到 $\mathcal O(qn^2)$ 或者 $\mathcal O(qn)$。
把上面的过程看成折线,可以发现要求的就是横坐标以下的面积。结合带修和数据范围,考虑分块维护,块内维护 $c_i$ 表示如果出发点是 $0$ 走到 $i$ 的个数,正负维护两个。查询时散块暴力,整块是前缀或者后缀和查询。修改散块暴力重构,整块只需要打一个正还是负的标记。复杂度 $\mathcal O(q\sqrt n)$。
Day ?
1. 在海的指尖
每位分别考虑贡献,现在需要计算第 $i$ 位为 $1$ 的方案数。
两个数相乘是在做 $(\mathrm{xor},\mathrm{and})$ 卷积:相邻两个数的第 $j$ 和 $i-j$ 位都是 $1$ 则会贡献到 $i$ 上。令 $j\leq i$,则所有的 $j$ 的贡献之间是独立的,可以分别计算。
设 $f_{k,0/1,0/1}$ 表示填了 $k$ 个,当前位是 $0/1$,贡献的异或和是 $0/1$ 的方案数。对于 $j$ 对 $i$ 的贡献,可以看成是从第 $X$ 位开始,分别是考虑的 $j,i-j,j,i-j\dots$ 位。转移显然是线性变换,写成矩阵的形式,设转移矩阵是 $M’$,做快速幂处理出 $M’^{X-1}$ 和 $M’^{n-X}$。
从小到大枚举 $i$,设 $a_{0/1}$ 表示当前的贡献异或和是 $0/1$ 的方案数。若 $Y$ 的第 $i$ 位是 $0$,则用初值 $f_{1,0}=1$ 的向量去乘两个转移矩阵,统计新的 $a_{0/1}$。复杂度 $\mathcal O(n+4^3\log n)$。
2. 只要梦还是「梦」的话
这我哪会啊。
3. Capella
这我哪会啊。
Day 7
1. 可爱小正太的必胜赌局
$a_i$ 表示只考虑赌 $A$ 的人,$A$ 赢了赔 $i$ 元时,$A$ 输了最多赚的钱数。$b_i,c_i$ 同理。做背包。
统计答案时,答案就是 $\min{b_j+c_k-i,a_i+c_k-j,a_i+b_j-k}$。变形一下 $a_i+b_j+c_k-\max{i+b_i,j+b_j,k+c_k}$。枚举 $\max{i+b_i,j+b_j,k+c_k}$ 计算。复杂度 $\mathcal O(n^2V)$。
2. 洛谷波特的挖河道计划
考虑调整法。调整你妈,调不了一点。
判掉无解,对于没有奇点,钦定所有四度点都是两条直线。这样跑欧拉回路会跑出来若干条环。合并两个环会造成 $2$ 的代价。如果环数 $=1$ 还要额外加 $2$ 的代价作为起点终点,否则可以把起点和终点设成拐弯的四度点。
对于有奇点的情况,如果有三度点,枚举它开始走哪条边暴力做最多九遍可以看成是一度点。还是做上面的过程就会跑出来一条链和若干个环,合并的代价还是 $2$。复杂度随便写都能过。
3. 人类为人类而写的文字
这我哪会啊。
Day 8
1. 开关灯
设 $f_{i,j}$ 表示操作了 $i$ 次,有 $j$ 个为 $1$,不允许相同的方案数。转移:
\[\begin{aligned} f_{i,j+3}&\overset +\leftarrow \binom{n-j}{3}f_{i,j}\\ f_{i,j+1}&\overset +\leftarrow \binom{n-j}{2}\binom{j}{1}f_{i,j}\\ f_{i,j-1}&\overset +\leftarrow \binom{n-j}{1}\binom{j}{2}f_{i,j}\\ f_{i,j-3}&\overset +\leftarrow \binom{j}{3}f_{i,j}\\ f_{i,j}&\overset -\leftarrow (i-1)f_{i-2,j} \end{aligned}\]最后是做了一个小荣斥。不是大荣斥,是小荣斥。最后答案需要除以 $m!$。
2. 森林
插头 DP。
3. 棋盘翻转
暴力做高消就爆了。发现只要确定了第一行后面的都能确定,可以把后面行的变量用第一行的变量表示出来,这样再做高消是 $\mathcal O(\frac{nm^3}{w})$。
Day 9
1. 超级宠物
自己想出来的,感觉自己很厉害/kx。把魔法变成强制异或所有的 $a_i$,和可以异或 $a_i\oplus b_i$,建出每个宠物 $i$ 的线性基 $S_i$。这样就能做 $l=r$ 的情况。
区间查询,$x$ 先和 $\oplus_{i=l}^rA_i$ 异或,幸运数全相等是平凡的,是查询区间线性基,感觉和正解关联不大啊?
对于幸运数不全相等的情况,从后向前扫。对于最后一个宠物,它能控制的只有他的线性基有值的位置,其他位置只能听天由命。对于倒数第二个宠物,它线性基中每一个数的每一个最后一个宠物有值的位置都没有用了,可以全部设成 $0$,然后再跑一遍线性基。现在新跑出来的主元就是这个宠物能控制的位置,依此类推。
可以发现这样只有 $\mathcal O(\log V)$ 个宠物是有用的,扫描线右端点,维护当前的线性基。每新加入一个,就把所有数的主元位置都消去,这样得到了新的 $\log V$ 个数。然后按照右端点从大到小排序加入线性基即可。
这样就可以找出这 $\mathcal O(\log V)$ 只宠物以及他们能控制的位置。查询的时候就从后向前做,每次选局部最优策略即可。瓶颈在于线性基暴力重建,复杂度是 $\mathcal O((n+q)\log V+c\log^2 V)$。
2. 回文计数
非常遗憾,没有遇见过的套路。暴力状压是 $\mathcal O(2^n n^2)$。考虑每次枚举最小的没有被填的位,找和他匹配的点。这样状态数是 $\sum_k\binom{n-k}{k}\approx\mathcal O((1.618)^n)$,只有大概一千万个,哈希表存状态,能过很多分。
正解有点神奇?把 $(1,2),(3,4),(5,6)\dots$ 匹配,这样加上匹配的边就变成了若干个环,并且这样状态数是 $\mathcal O(2^{\frac n 2})$。设 $g_{S,i}$ 表示当前集合内有哪些点对,当前环的起点是 $S$ 中最小的点,$i$ 环的另一端。转移是加入一个 pair,注意需要满足加入的 pair 都大于 $S$ 中最小的点才能保证去重。
这样可以求出 $G_S$ 表示 $S$ 中构成一个环的权值和。对 $G$ 代表做一个集合幂级数 exp,这样全集就是答案。暴力做是 $\mathcal O(3^{\frac n 2})$ 的,也可以做到 $\mathcal O(2^{\frac n 2}n^2)$。
有点看不懂中间这一步匹配转环的本质是啥啊。
3. 最优组合
首先对于两条链,先求出各自权值和,这样答案一定跨过了权值和较大的权值终点。
建出坐标系,横轴表示第一个序列,纵轴表示第二个序列,则问题就是有一些点,选一个矩形不能包含任何的点,要求矩形权值和最大。假定矩形一定跨过横轴的中点,则可以对纵轴扫描线,扫描线矩形上边界,则左右两部分的下边界取值都是一个单调栈,复杂度是 $\mathcal O((n+m)\log n)$。这样总复杂度是 $\mathcal O(20^2(n+m)\log n)$。有 $60$。跑路。
很有点分治的感觉。点分一下,$x$ 点到根的路径会把序列分成若干个区间。结论是要求 $x$ 的所有儿子都在一个区间里 $x$ 才仅在这个区间上有用。如果不都在一个区间里,则一定可以向没有取到答案的区间中的儿子中走的更深,权值更大。
把这个结论再推广一下,需要选取两个不同子树内的点 $u,v$,满足 $w_u+w_v+S([l_u,r_u]\cap[l_v,r_v])$ 最大,$S$ 指序列权值。是一个简单的二维数点。要求来自两个不同子树可以同时记录颜色不同的最大和次大值。对于 $u,v$ 取到叶子的情况可以直接暴力,还要判掉只在树上或者是序列上选数的情况。复杂度 $\mathcal O(n\log^2 n+m\log n)$。