提供一个不用动脑子的方法。
首先题目可以看成是求一个点到 $s$ 的最小瓶颈路,设这个值为 $v_i$,自然想到最小生成树,但是边数是 $\mathcal O(n^2)$ 的,不可接受。
考虑使用 prim,一开始联通块里只有一个点 $s$,每次新加入距离联通快距离最小的一个点,问题在于如何找到全局最小值。
直接求肯定没有前途,考虑加入一个点对其他点 $v_i$ 的贡献:
\[v_j=\min(v_j,\max(v_i,\min(\lvert a_j-(a_i-d)\rvert,\lvert a_j-(a_i+d)\rvert)))\]然后可以把 $\max$ 和绝对值暴力拆开,可以变成区间 $v_i=\min(v_i,x-a_i)$ 和 $v_i=\min(v_i,x+a_i)$ 和 $v_i=\min(v_i,x)$。图大概就是这样的:
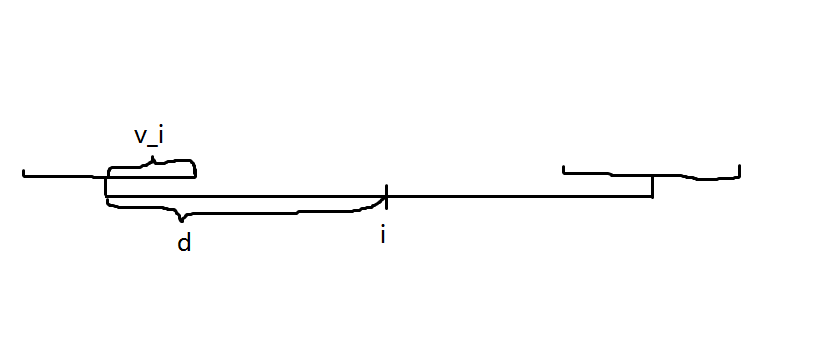
线段树维护区间 $a_i$ 最大值最小值,当前 $v_i$ 最小值及其位置即可,每次找到最小值的位置更新真实的 $v_i$ 然后删掉这个位置,复杂度 $\mathcal O(n\log n+m)$。常数也不算大。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
int n,m,S,d,v[200010],a[200010];
namespace Segment
{
struct{int l,r,tg1,tg2,tg3;pii mina,maxa,minn;}t[800010];
inline pii chkmin(pii p1,pii p2){if(!~p2.se)return p1;if(!~p1.se)return p2;return p1.fi<p2.fi?p1:p2;}
inline pii chkmax(pii p1,pii p2){if(!~p2.se)return p1;if(!~p1.se)return p2;return p1.fi>p2.fi?p1:p2;}
inline void update(int p)
{
t[p].mina=chkmin(t[p*2].mina,t[p*2+1].mina);
t[p].maxa=chkmax(t[p*2].maxa,t[p*2+1].maxa);
t[p].minn=chkmin(t[p*2].minn,t[p*2+1].minn);
}
inline void down1(int p,int x)
{
Mmin(t[p].tg1,x);
if(x+t[p].mina.fi<t[p].minn.fi)t[p].minn=mp(x+t[p].mina.fi,t[p].mina.se);
}
inline void down2(int p,int x)
{
Mmin(t[p].tg2,x);
if(x-t[p].maxa.fi<t[p].minn.fi)t[p].minn=mp(x-t[p].maxa.fi,t[p].maxa.se);
}
inline void down3(int p,int x){Mmin(t[p].tg3,x),Mmin(t[p].minn.fi,x);}
inline void spread(int p)
{
if(t[p].tg1!=inf)down1(p*2,t[p].tg1),down1(p*2+1,t[p].tg1);
if(t[p].tg2!=inf)down2(p*2,t[p].tg2),down2(p*2+1,t[p].tg2);
if(t[p].tg3!=inf)down3(p*2,t[p].tg3),down3(p*2+1,t[p].tg3);
t[p].tg1=t[p].tg2=t[p].tg3=inf;
}
void build(int p,int l,int r)
{
t[p].l=l,t[p].r=r,t[p].tg1=t[p].tg2=t[p].tg3=inf;
if(l==r)return t[p].mina=t[p].maxa=mp(a[l],l),t[p].minn=mp(inf,l),void();
int mid=l+((r-l)>>1);
build(p*2,l,mid),build(p*2+1,mid+1,r),update(p);
}
void change(int p,int x)
{
if(t[p].l==t[p].r)
return t[p].mina=mp(inf,-1),t[p].maxa=mp(-inf,-1),t[p].minn=mp(inf,-1),void();
spread(p);
if(x<=t[p*2].r)change(p*2,x);else change(p*2+1,x);
update(p);
}
void modify1(int p,int l,int x)
{
if(l<=t[p].l)return down1(p,x);
spread(p),modify1(p*2+1,l,x);
if(l<=t[p*2].r)modify1(p*2,l,x);
update(p);
}
void modify2(int p,int r,int x)
{
if(r>=t[p].r)return down2(p,x);
spread(p),modify2(p*2,r,x);
if(r>t[p*2].r)modify2(p*2+1,r,x);
update(p);
}
void modify3(int p,int l,int r,int x)
{
if(l<=t[p].l&&r>=t[p].r)return down3(p,x);
spread(p);
if(l<=t[p*2].r)modify3(p*2,l,r,x);
if(r>t[p*2].r)modify3(p*2+1,l,r,x);
update(p);
}
void print(int p)
{
if(t[p].l==t[p].r)return write(t[p].minn.fi,' ');
spread(p),print(p*2),print(p*2+1);
}
}
using namespace Segment;
inline void mian()
{
read(n,m,S,d);int x,y;
for(int i=1;i<=n;++i)read(a[i]);
build(1,1,n),memset(v,127,sizeof(v)),change(1,S),v[S]=0;
for(int i=1;i<=n;++i)
{
int pos1=lower_bound(a+1,a+1+n,a[S]-d-v[S])-a;
int pos2=upper_bound(a+1,a+1+n,a[S]-d+v[S])-a-1;
if(pos1<=pos2&&pos1>=1&&pos2<=n)
modify3(1,pos1,pos2,v[S]);
if(pos1-1)modify2(1,pos1-1,a[S]-d);
if(pos2<n)modify1(1,pos2+1,d-a[S]);
pos1=lower_bound(a+1,a+1+n,a[S]+d-v[S])-a;
pos2=upper_bound(a+1,a+1+n,a[S]+d+v[S])-a-1;
if(pos1<=pos2&&pos1>=1&&pos2<=n)
modify3(1,pos1,pos2,v[S]);
if(pos1-1)modify2(1,pos1-1,d+a[S]);
if(pos2<n)modify1(1,pos2+1,-d-a[S]);
v[S=t[1].minn.se]=t[1].minn.fi,change(1,S);
}
while(m--)read(x,y),puts(y<v[x]?"No":"Yes");
}