[ARC150F] Constant Sum Subsequence
很有意思的题。
设 $nex_{i,j}$ 表示位置 $i$ 后面的最小的满足 $k>i\wedge a_k=j$ 的 $k$,则问题可以抽象为:
\[f_i=\max_{j=1}^inex_{f_{i-j},j}\]直接做是 $\mathcal O(S^2\log S)$ 的。这个东西也不像是用线段树之类的东西可以优化的,打表发现也没有决策单调性,考虑从问题本身入手。
关键性质:$f$ 严格单调递增。证明很简单,可以在 $f_{i-1}$ 对应的子序列后面加一个 $1$,所以 $f_i>f_{i-1}$。
考虑用类似 CDQ 分治的思路,分治计算 $f$。假设当前计算 区间 $[l,r]$,先计算左半边 $[l,\lfloor\frac{l+r}{2}\rfloor]$,然后考虑左对右的贡献,然后计算右半边 $[\lfloor\frac{l+r}{2}\rfloor+1,r]$。
因为 $f$ 是单调递增的,所以 $\forall i\in[\lfloor\frac{l+r}{2}\rfloor+1,r],f_i>f_{mid}$。考虑对于每一个 $j$,左半边的 $nex$ 应当是这样的:
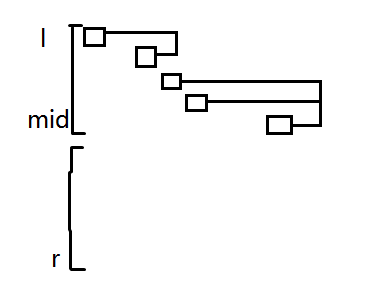
其中上下位置代表 $[l,r]$,小方格的左右位置代表 $f_i$,向右的线表示 $nex_{f_i,j}$。注意到左上角的两个 $f$ 一定没有贡献,有贡献的一定是最右边的一段区间,这时候可以 seg beats 直接做了,但是其实还是没有必要。因为 $f$ 严格单增,所以我们只需要考虑第三个小方格的贡献即满足 $nex_{f_i,j}=nex_{f_{mid},j}$ 的最小的 $i$,因为用 $f_i$ 去更新 $f_{i+j}$ 之后不可能用 $f_{i+1}$ 去更新 $f_{i+j+1}$,因为两者的 $nex$ 是一样的。所以只需要枚举每一个 $j$,找到满足要求的最小的 $i$ 去更新右半部分的数组即可,需要注意边界问题。复杂度 $\mathcal O(S\log S\log n)$,代码并不难写。
注意观察性质可以使问题得到很大的简化。其中分治的本质是找到一个合适的分界线来寻找最优决策点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
int n,m,a[1500010],lst[200010],pr[1500010],f[200010];
vector<int> ve[200010];
inline int nex(int i,int j)
{
auto it=upper_bound(ve[j].begin(),ve[j].end(),(i-1)%n+1);
if(it==ve[j].end())return ve[j].front()+((i-1)/n+1)*n;
return *it+(i-1)/n*n;
}
int find(int L,int R,int x)
{
int mid;
while(L<R)
{
mid=L+((R-L)>>1);
if(f[mid]>=x)R=mid;
else L=mid+1;
}
return L;
}
void solve(int l,int r)
{
if(l==r)return;
int mid=l+((r-l)>>1),pos,pre;
solve(l,mid);
for(int i=1;i<=r-l;++i)
{
pos=nex(f[mid],i),pre=(pos-1)/n*n+pr[(pos-1)%n+1];
pre=find(l,mid,pre);
if(pre+i>r)continue;
pre=max(pre,mid+1-i);
assert(pre+i>mid);
assert(pre+i<=r);
assert(nex(f[pre],i)==pos);
assert(pre==l||nex(f[pre-1],i)!=pos);
f[pre+i]=max(f[pre+i],pos);
}
solve(mid+1,r);
}
inline void mian()
{
read(n,m);
for(int i=1;i<=n;++i)read(a[i]),ve[a[i]].eb(i);
for(int i=1;i<=n;++i)lst[a[i]]=i-n;
for(int i=1;i<=n;++i)pr[i]=lst[a[i]],lst[a[i]]=i;
solve(0,m),write(f[m]);
}