设 $f(x,y)$ 表示树上 $x$ 到 $y$ 简单路径上的点权或和中 $1$ 的个数。
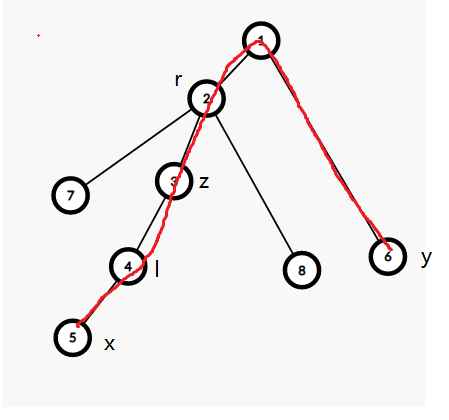
有一个性质:选取的 $z$ 节点一定满足它比它左边的点($l$)或者右边的点($r$)的贡献至少要多一位,即 $f(x,l)<f(x,z)$ 或 $f(y,r)<f(y,z)$,有了这个性质,问题就简单很多了。
即 $d_{i,j}$ 表示第 $i$ 个点的祖先中满足第 $j$ 位为 $1$ 的最深节点的编号,把 $x$ 到 $y$ 的路径看成 $x$ 到 $lca$ 和 $y$ 到 $lca$ 的两段,考虑 $z$ 在第一段路径上,只需要枚举 $d_{x,i}$ 和 $d_{y,i}$ 并检查是否合法(深度大于等于 LCA)然后暴力计算即可,对于 $z$ 在第二段路径上的情况同理。
代码中使用倍增实现求 $LCA$ 和一段路径的或和,复杂度为 $\mathcal O(n\log n \log V)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
int cnt,T,q,maxn,n,v[200001][21],d[200001][31],dep[200001],a[200001],fa[200001][21],head[200001],to[400001],nex[400001];
inline void add(int x,int y){to[++cnt]=y,nex[cnt]=head[x],head[x]=cnt;}
void dfs(int k,int fat)
{
fa[k][0]=fat,memcpy(d[k],d[fat],sizeof(d[k])),dep[k]=dep[fat]+1,v[k][0]=a[k];
for(int i=0;i<=30;++i)if(a[k]>>i&1)d[k][i]=k;
for(int i=1;i<=20;++i)fa[k][i]=fa[fa[k][i-1]][i-1],v[k][i]=v[k][i-1]|v[fa[k][i-1]][i-1];
for(int i=head[k];i;i=nex[i])if(to[i]!=fat)dfs(to[i],k);
}
inline int LCA(int x,int y)
{
if(dep[x]>dep[y])swap(x,y);
for(int i=20;i>=0;--i)if(dep[fa[y][i]]>=dep[x])y=fa[y][i];
for(int i=20;i>=0;--i)if(fa[y][i]!=fa[x][i])y=fa[y][i],x=fa[x][i];
return x==y?x:fa[x][0];
}
inline int ask(int x,int fat)
{
int ans=0;
for(int i=20;i>=0;--i)if(dep[fa[x][i]]>=dep[fat])ans|=v[x][i],x=fa[x][i];
return ans|v[fat][0];
}
void mian()
{
read(T);int x,y,lca,vx,vy;
while(T--)
{
read(n),memset(head,0,sizeof(head)),cnt=0,maxn=0;
for(int i=1;i<=n;++i)read(a[i]);
for(int i=1;i<n;++i)read(x,y),add(x,y),add(y,x);
dfs(1,0),read(q);
while(q--)
{
read(x,y),lca=LCA(x,y),maxn=0,vx=ask(x,lca),vy=ask(y,lca);
for(int i=0;i<=30;++i)if(d[x][i]&&dep[d[x][i]]>=dep[lca])maxn=max(maxn,__builtin_popcount(vy|ask(d[x][i],lca))+__builtin_popcount(ask(x,d[x][i])));
for(int i=0;i<=30;++i)if(d[y][i]&&dep[d[y][i]]>=dep[lca])maxn=max(maxn,__builtin_popcount(vx|ask(d[y][i],lca))+__builtin_popcount(ask(y,d[y][i])));
write(maxn);
}
puts("");
}
}