AT_ddcc2020_final_d Pars/ey
重工业题。
找环然后树形 DP 是显然的,先考虑断开环上的边怎么做。
把环复制一遍放在结尾,记 $sum_i$ 为环长的前缀和,$f_i$ 为该子树内的最长根链的长度,问题变为每次给定一个区间,要求找到 $i,j(i>j)$ 使得 $sum_i-sum_j+f_i+f_j$ 最大,可以使用线段树实现。注意要与同一棵树里的直径取 max(大概有 $\mathcal O(n)$ 做法吧)
然后考虑树边如何处理。先求出不删边时基环树的直径,如果是树内的直径那么删其他边不会对答案造成影响,所以只需计算该子树。直径经过了环可以对两个端点所在的树计算两次。
断了树边后基环树的直径有 2 种情况:直径至少有一端在这棵树里和不在这棵树里。两端都在树外面是好处理的,对于第一种情况可以类似换根的方法处理。
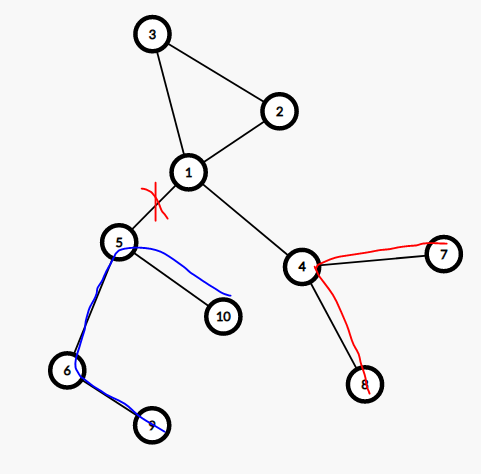
1.直径为蓝色或红色的路径。
蓝色的路径是好处理的,对于每棵子树维护子树内直径即可。
对于红色,因为换根到儿子时红色路径的长度可以继承父亲的,所以只需要一个变量记录当前红色路径的长度。
设当前最长的红色路径长度为 $dead$,设 $in_{k,0}$ 表示以 $k$ 为根的子树内不经过该点的最大直径, $in_{k,1}$ 表示和 $in_{k,0}$ 不在同一棵子树里的最大直径,这样向下搜索时如果 $to$ 是 $in_{k,0}$ 所在的子树,用 $in_{k,1}$ 更新 $dead$,否则用 $in_{k,0}$ 更新。
另一种情况,如下图:这条红色路径的可以在 $5$ 号点是更新,具体的,类似换根 DP 的思路,我们记 $maxn$ 表示当前点向父亲走能走到的最远的距离(树内),用 $maxn+f_k$ 更新红色路径的长度。但是更新时会出现问题:$f_5$ 本身由 $f_6$ 转移而来,所以我们不仅要记录最长根链的长度,还要记录和最长根链不在同一子树内的次长根链的长度,如果 $f_{to,0}+v_i$ 和 $f_{k,0}$ 相等,用 $f_{k,1}+maxn$ 更新红色路径,否则用 $f_{to,0}$ 更新。
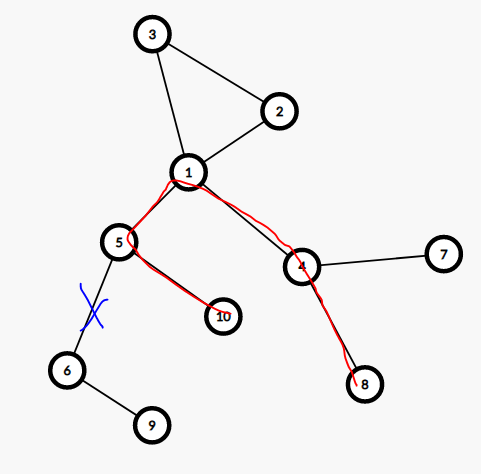
另另一种情况,如下图:断掉了 $(1,5)$,$dead$ 还可以由 $1$ 子树内不经过 $5$ 的两条链拼接而成,所以我们不仅要记录次大根链,还要记录次次大根链,如果断的边是 $f_{k,0}$ 的链,用 $f_{k,1}+f_{k,2}$ 更新 $dead$,其他情况同理。
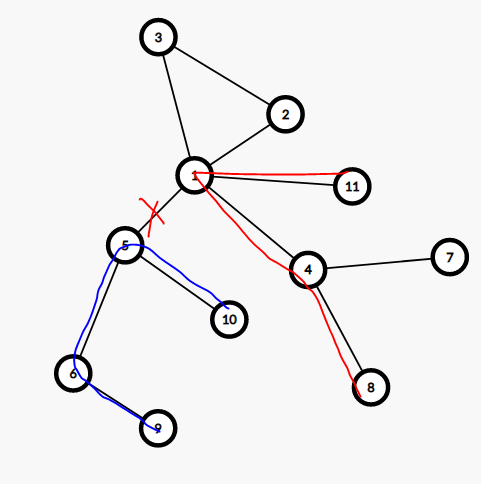
2.直径另一端不在该树内。
这种情况是 trival 的,记录 $up$ 表示该点到根的距离,每次向下走维护到根的距离的最大值和当前到根的距离,每次还是判断最大次大值与子树的值的关系即可。
细节很多,非常难写。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
int n,cnt=1,dead,tot,max2,all,now,now2,maxu,maxi,maxj,ans[800001],pos[800001],id[800001],ide[800001],in[800001][2],f[800001][3],ex[800001],vis[800001],loop[800001],head[800001],to[800001],nex[800001],v[800001],sum[800001],val[800001];
inline void add(int x,int y,int z){to[++cnt]=y,v[cnt]=z,nex[cnt]=head[x],head[x]=cnt;}
stack<int> st;
namespace Segment
{
struct Node{int maxn,max1,max2,l,l1,r,r2;};
struct{int l,r;Node nd;}t[3400001];
Node operator +(const Node nd1,const Node nd2)
{
Node nd;nd.l=nd1.l1,nd.r=nd2.r2,nd.maxn=nd1.max1+nd2.max2;
if(nd1.maxn>nd.maxn)nd.maxn=nd1.maxn,nd.l=nd1.l,nd.r=nd1.r;
if(nd2.maxn>nd.maxn)nd.maxn=nd2.maxn,nd.l=nd2.l,nd.r=nd2.r;
if(nd1.max1>nd2.max1)nd.l1=nd1.l1;else nd.l1=nd2.l1;nd.max1=max(nd1.max1,nd2.max1);
if(nd1.max2>nd2.max2)nd.r2=nd1.r2;else nd.r2=nd2.r2;nd.max2=max(nd1.max2,nd2.max2);
return nd;
}
void build(int p,int l,int r)
{
t[p].l=l,t[p].r=r;
if(l==r)return t[p].nd.l=t[p].nd.l1=t[p].nd.r=t[p].nd.r2=l,val[l]+=val[l-1],t[p].nd.max2=f[loop[l]][0]+val[l-1],t[p].nd.max1=f[loop[l]][0]-val[l-1],void();
int mid=l+((r-l)>>1);
build(p*2,l,mid),build(p*2+1,mid+1,r),t[p].nd=t[p*2].nd+t[p*2+1].nd;
}
void change(int p,int x,int y)
{
if(t[p].l==t[p].r)return t[p].nd.max2=y+val[x],t[p].nd.max1=y-val[x],void();
if(x<=t[p*2].r)change(p*2,x,y);else change(p*2+1,x,y);
t[p].nd=t[p*2].nd+t[p*2+1].nd;
}
Node ask(int p,int l,int r)
{
if(l<=t[p].l&&r>=t[p].r)return t[p].nd;
if(l>t[p*2].r)return ask(p*2+1,l,r);
if(r<=t[p*2].r)return ask(p*2,l,r);
return ask(p*2,l,r)+ask(p*2+1,l,r);
}
void print(int p)
{
if(!t[p].l)return;
write(t[p].l),write(t[p].r),write(t[p].nd.max1),write(t[p].nd.max2),write(t[p].nd.maxn,'\n');
print(p*2),print(p*2+1);
}
}
using namespace Segment;
void findloop(int k,int from)
{
st.e(k);
for(int i=head[k];i;i=nex[i])
{
if(i==(from^1))continue;
if(sum[to[i]])
{
int y;sum[k]=v[i],ide[k]=i;
do vis[loop[++tot]=y=st.top()]=1,id[tot]=ide[y],val[tot]=sum[y],st.pop();while(y!=to[i]);
}
else sum[k]=v[i],ide[k]=i,findloop(to[i],i);
if(tot)return;
}
st.pop();
}
void dfs(int k,int from)
{
for(int i=head[k];i;i=nex[i])
{
if(i==(from^1)||vis[to[i]])continue;
dfs(to[i],i);int tmp=max(in[to[i]][0],f[to[i]][0]+f[to[i]][1]);
if(tmp>=in[k][0])in[k][1]=in[k][0],in[k][0]=tmp;
else if(tmp>=in[k][1])in[k][1]=tmp;
if(f[to[i]][0]+v[i]>=f[k][0])f[k][2]=f[k][1],f[k][1]=f[k][0],f[k][0]=f[to[i]][0]+v[i];
else if(f[to[i]][0]+v[i]>=f[k][1])f[k][2]=f[k][1],f[k][1]=f[to[i]][0]+v[i];
else if(f[to[i]][0]+v[i]>=f[k][2])f[k][2]=f[to[i]][0]+v[i];
}
}
inline void dfs2(int k,int maxn,int from,int up)
{
int pre=maxu,ppr=dead;
// write(k),write(dead,'\n');
for(int i=head[k],upon;i;i=nex[i])
{
if(vis[to[i]]||i==(from^1))continue;
if(in[to[i]][0]==in[k][0]||f[to[i]][0]+f[to[i]][1]==in[k][0])dead=max(dead,in[k][1]);
else dead=max(dead,in[k][0]);
// write(to[i]),write(in[k][0]),write(in[k][1]),write(dead,'\n');
if(f[to[i]][0]+v[i]==f[k][0])dead=max({dead,f[k][1]+maxn,f[k][1]+f[k][2]});
else if(f[to[i]][0]+v[i]==f[k][1])dead=max({dead,f[k][0]+maxn,f[k][0]+f[k][2]});
else dead=max({dead,f[k][0]+f[k][1],maxn+f[k][0]});
// write(to[i]),write(dead,'\n');
if(f[to[i]][0]+v[i]==f[k][0])upon=f[k][1],maxu=max(maxu,up+f[k][1]),dfs2(to[i],max(maxn,f[k][1])+v[i],i,up+v[i]);
else upon=f[k][0],maxu=max(maxu,up+f[k][0]),dfs2(to[i],max(maxn,f[k][0])+v[i],i,up+v[i]);
ans[pos[i]]=max({dead,in[to[i]][0],f[to[i]][0]+f[to[i]][1],now+max(maxu,upon+up),now2});
if(f[to[i]][0]+v[i]==f[k][0])ans[pos[i]]=max({ans[pos[i]],f[k][1]+f[k][2],f[k][1]+maxn});
else if(f[to[i]][0]+v[i]==f[k][1])ans[pos[i]]=max({ans[pos[i]],f[k][0]+f[k][2],f[k][0]+maxn});
else ans[pos[i]]=max({ans[pos[i]],f[k][0]+f[k][1],f[k][0]+maxn});
maxu=pre,dead=ppr;
}
// write(k),write(dead,'\n');
}
inline Node calc2()
{
Node nd1,nd2;nd1.maxn=0;
for(int i=2,j=1;i<=tot*2;++i)
{
while((val[i]-val[j])*2>all)++j;
nd2=ask(1,j,i);if(nd2.maxn>nd1.maxn)nd1=nd2;
}
return nd1;
}
inline void calc(int ex)
{
if(ex>tot)ex-=tot;
change(1,ex,0),change(1,ex+tot,0),dead=0;
now=-INF,now2=calc2().maxn;
for(int i=1;i<=tot;++i)if(i!=ex)now2=max({now2,in[loop[i]][0],f[loop[i]][0]+f[loop[i]][1]});
for(int i=ex+tot-1;i>ex;--i)if((val[i]-val[ex])*2<=val[tot+1])now=max(now,val[i]+f[loop[i]][0]-val[ex]);
for(int i=ex+1;i<ex+tot;++i)if((val[ex+tot]-val[i])*2<=val[tot+1])now=max(now,f[loop[i]][0]-val[i]+val[ex+tot]);
dfs2(loop[ex],0,0,0);
change(1,ex,f[loop[ex]][0]),change(1,ex+tot,f[loop[ex]][0]);
}
inline void mian()
{
read(n);int x,y,z,pos2=0;Node nd;
for(int i=1;i<=n;++i)read(x,y,z),add(x,y,z),add(y,x,z),pos[cnt]=pos[cnt-1]=i;
findloop(1,0),reverse(loop+1,loop+tot+1),reverse(val+1,val+tot+1),reverse(id+1,id+1+tot),id[0]=id[tot];
for(int i=1;i<=tot;++i)loop[i+tot]=loop[i],val[i+tot]=val[i],now=i,dfs(loop[i],0),max2=max({max2,in[loop[i]][0],f[loop[i]][0]+f[loop[i]][1]}),max(in[loop[i]][0],f[loop[i]][0]+f[loop[i]][1])==max2?pos2=i:0;
build(1,1,tot*2),all=val[tot];
for(int i=tot*2;i>=1;--i)val[i]=val[i-1];
nd=calc2();
for(int i=1;i<=tot;++i)ans[pos[id[i-1]]]=max(max2,ask(1,i,i+tot-1).maxn);
if(nd.maxn<=max2)calc(pos2);else calc(nd.l),calc(nd.r);
for(int i=1;i<=n;++i)if(!ans[i])write(max(nd.maxn,max2),'\n');else write(ans[i],'\n');
}