感觉很神奇的题。
一条路径的代价是前 $k$ 大的边的权值和,有个假的做法是每个点维护一个堆,表示走到这个点前 $k$ 大边的权值,读者可以思考一下这个做法为什么是假的。
既然直接最短路不好处理,自己观察性质,可以发现前 $k$ 条边权值和等价于每条边边权变为 $\max(val-val_k,0)$,然后跑最短路后 $dis_n+k\times val_k$。
一开始的想法是三分,因为感觉这个东西是凸的。
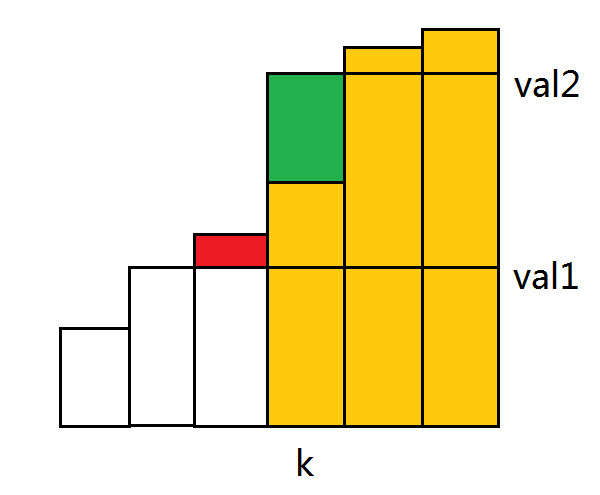
上图的矩形高度代表一条路径每条边的权值(已进行排序),显然黄色的部分是实际的路径权值。
如果你选的 $val_1 < val_k$,那么相当于多算了红色的部分。而如果选的 $val_2>val_k$,那么相当于多算了绿色的部分,所以这个函数是凸的(感性理解)。
但是如果直接三分会有问题,这个函数可能有连续函数值相等的一段,所以不能三分。
发现 $val$ 只有在等于原图中边的权值才是有意义的,结合数据范围,可以直接枚举每一条边作为 $val_k$,取最小值。
注意题目要求:如果经过的边数小于 $k$,权值为路径权值,所以先跑一边 dijistra,初始答案为 $dis_n$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int n,m,p,cnt,l,r,mid,ans=INF,vis[3001],d[3001],e[3001],head[3001],v[6001],to[6001],nex[6001],numa[6001];
inline void add(int x,int y,int z){to[++cnt]=y,v[cnt]=z,nex[cnt]=head[x],head[x]=cnt;}
priority_queue<pii> q;
void dijkstra(int val)
{
q.e(mp(0,1)),memset(d,127,sizeof(d)),memset(vis,0,sizeof(vis)),d[1]=0;
while(!q.empty())
{
int now=q.top().se;q.pop();
if(vis[now])continue;
vis[now]=1;
for(int i=head[now],va;i;i=nex[i])
{
va=max(v[i]-val,0ll);
if(d[to[i]]>d[now]+va)
d[to[i]]=d[now]+va,q.e(mp(-d[to[i]],to[i]));
}
}
}
inline void mian()
{
read(n,m,p);int x,y,z;
for(int i=1;i<=m;++i)read(x,y,z),numa[i]=z,add(x,y,z),add(y,x,z);
sort(numa+1,numa+1+m);
dijkstra(0),ans=d[n];
for(int i=1;i<=m;++i)if(numa[i]!=numa[i-1])dijkstra(numa[i]),ans=min(ans,d[n]+p*numa[i]);
write(ans);
}