点仙人掌的性质:每个点最多只在一个环里。
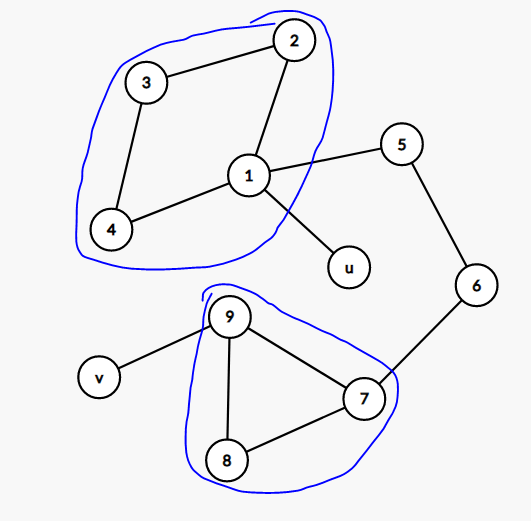
对于 $u,v$ 之间的路径,显然一定是由一些链和一些环拼接而成的。
对于链,只能按照唯一的方式行走。
对于环,有两种走的方案:顺时针和逆时针走。
各个环间互不影响,乘法原理得到答案就是 $2$ 的环个数次方。
边双所点后维护前缀和,变成树上 LCA 问题,倍增或树剖或 tarjan 即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
inline int power(int x,int y)
{
int ans=1;
for(;y;x=x*x%MOD,y>>=1)if(y&1)ans=ans*x%MOD;
return ans;
}
int n,m,q,tot,cnt,num,col[300001],val[300001],dep[300001],fa[300001][21],x[300001],y[300001],dfn[300001],low[300001],cut[200001],head[300001],to[500001],nex[500001];
vector<int> T[300001];
stack<int> st;
inline void add(int x,int y){to[++cnt]=y,nex[cnt]=head[x],head[x]=cnt;}
void tarjan(int k,int from)
{
dfn[k]=low[k]=++tot,st.push(k);
for(int i=head[k];i;i=nex[i])
{
if(i==(from^1))continue;
if(!dfn[to[i]])
{
tarjan(to[i],i),low[k]=min(low[k],low[to[i]]);
if(low[to[i]]>dfn[k])cut[i]=cut[i^1]=1;
}
else low[k]=min(low[k],dfn[to[i]]);
}
if(dfn[k]==low[k])
{
col[k]=++num;int y=1;
while(st.top()!=k)++y,col[st.top()]=num,st.pop();
st.pop();
if(y>1)val[num]=1;
}
}
void dfs(int k,int father)
{
val[k]+=val[father],dep[k]=dep[father]+1,fa[k][0]=father;
for(int i=1;i<=20;++i)fa[k][i]=fa[fa[k][i-1]][i-1];
for(auto to:T[k])if(to!=father)dfs(to,k);
}
inline int LCA(int x,int y)
{
if(dep[x]>dep[y])swap(x,y);
for(int i=20;i>=0;--i)if(dep[fa[y][i]]>=dep[x])y=fa[y][i];
for(int i=20;i>=0;--i)if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
return x==y?x:fa[x][0];
}
inline void mian()
{
cnt=1,read(n,m);int a,b,lca;
for(int i=1;i<=m;++i)read(x[i],y[i]),add(x[i],y[i]),add(y[i],x[i]);
for(int i=1;i<=n;++i)if(!dfn[i])tarjan(i,0);
for(int i=1;i<=m;++i)if(col[x[i]]!=col[y[i]])T[col[x[i]]].eb(col[y[i]]),T[col[y[i]]].eb(col[x[i]]);
dfs(1,0),read(m);
while(m--)read(a,b),a=col[a],b=col[b],lca=LCA(a,b),write(power(2,val[a]+val[b]-val[lca]-val[fa[lca][0]]),'\n');
}