自然的想法是枚举共同的交点,然后进行换根 dp,复杂度可以做到 $\mathcal O(n^2)$,可以通过简单版,但是显然过不了 $10^5$ 的数据,考虑进行优化。
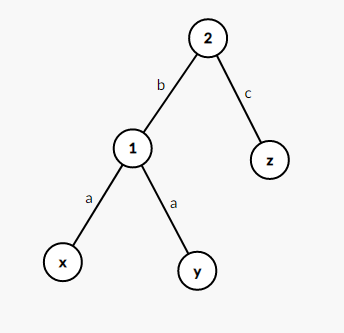
记 $(x,y,z)$ 为满足要求的点,即满足 $a=b+c$,树形 dp 原则是子树内的信息无后效性,尽量把子树内的信息合并在一起。所以 $a-b=c$,在这个等式种,$a-b$ 和 $c$ 在以 $2$ 为根的两棵不同子树,所以转变统计方式,在 $2$ 号统计答案。
设计状态 $g_{i,j}$ 表示 $i$ 子树内部满足 $a-b=j$ 的点对数量,因为要统计 $z$ 的数量,所以设 $f_{i,j}$ 表示 $i$ 子树内和 $i$ 距离为 $j$ 的点的个数。
状态明确了,方程是容易设计的:
\[\begin{aligned} f_{i,j}&=\sum_{u \in son_i}f_{u,j-1} \\ g_{i,j}&=\sum_{u \in son_i}g_{u,j+1}+f_{i,j}\times f_{u,j-1}\\ ans&=\sum_{u \in son_i}f_{i,j-1}\times g_{u,j}+g_{i,j}\times f_{u,j-1} \end{aligned}\]直接 dp 复杂度仍然是 $\mathcal O(n^2)$ 的,但是发现状态中 $j$ 只和深度有关,考虑使用长链剖分优化 dp。
观察方程,当只有一个儿子 $u$ 时,可以简化为:
\[\begin{aligned} f_{i,j}&=f_{u,j-1} \\ g_{i,j}&=g_{u,j+1} \\ ans&=g_{i,0} \end{aligned}\]可以先对重儿子进行 dp,重儿子的 dp 值平移一下直接给父亲用,具体实现使用指针,详见代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int n,head[100005],dep[100005],to[200005],son[100001],nex[200001],a[100001],cnt;
ll ans,*g[100005],*f[100005],p[400050],*o=p;
inline void add(int x,int y){to[++cnt]=y,nex[cnt]=head[x],head[x]=cnt;}
void dfs1(int k,int fa)
{
dep[k]=1;
for(int i=head[k];i;i=nex[i])
{
if(to[i]==fa)continue;
dfs1(to[i],k);
if(dep[to[i]]+1>dep[k])dep[k]=dep[to[i]]+1,son[k]=to[i];
}
}
void dfs(int k,int fa)
{
if(son[k])f[son[k]]=f[k]+1,g[son[k]]=g[k]-1,dfs(son[k],k);
f[k][0]=1,ans+=g[k][0];
for(int i=head[k];i;i=nex[i])
{
if(to[i]==fa||to[i]==son[k])continue;
f[to[i]]=o,o+=dep[to[i]]<<1,g[to[i]]=o,o+=dep[to[i]]<<1,dfs(to[i],k);
for(int j=0;j<dep[to[i]];++j)
{
if(j)ans+=f[k][j-1]*g[to[i]][j];
ans+=g[k][j+1]*f[to[i]][j];
}
for(int j=0;j<dep[to[i]];++j)
g[k][j+1]+=f[k][j+1]*f[to[i]][j],
f[k][j+1]+=f[to[i]][j],
g[k][j]+=g[to[i]][j+1];
}
}
inline void mian()
{
read(n);int x,y;
for(int i=1;i<n;++i)read(x,y),add(x,y),add(y,x);
dfs1(1,0),f[1]=o,o+=dep[1]<<1,g[1]=o,o+=dep[1]<<1,dfs(1,0),write(ans);
}